�@ ���w�Z���̍ō���A�咆�w��
���N�̖�肩��P�Љ�܂��B��N�͑�ϊȒP�ł������A
�@ ���w�Z���̍ō���A�咆�w��
���N�̖�肩��P�Љ�܂��B��N�͑�ϊȒP�ł������A
���N�͊u�N���ۂŗ\�z�ʂ����܂����B�Z���̒�ԁA���̂̐ؒf�ł��B
�悭�l�������قǓ���͂���܂���B
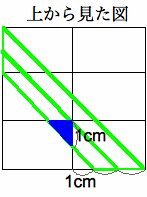
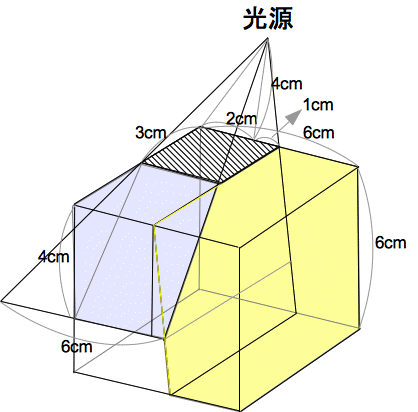
 [���]�@�@�ӂ̒�����1cm,2cm,3cm�̒����̂̌`�������A���g�̋l��
[���]�@�@�ӂ̒�����1cm,2cm,3cm�̒����̂̌`�������A���g�̋l��
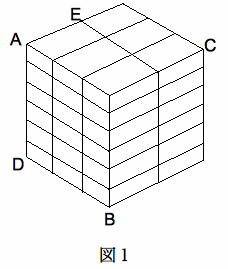
�����u���b�N36���E�̐}�P�̂悤�ɁA�ςݏd�˂āA�P�ӂ̒�����
6cm�̗����� ���� �� �܂����B�@
�@( �Q�O�P�R�N�咆�w�Q���ڂT��)
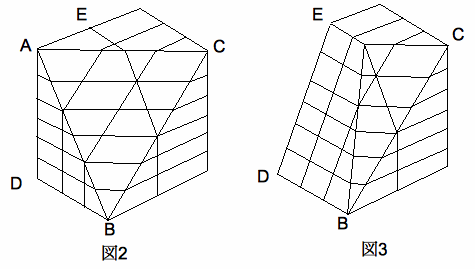
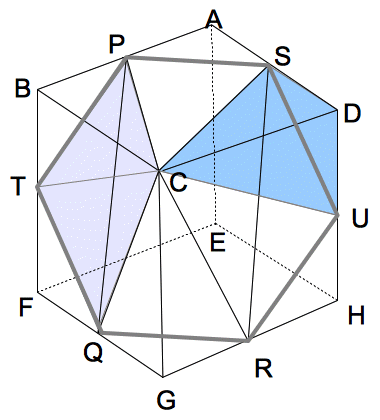
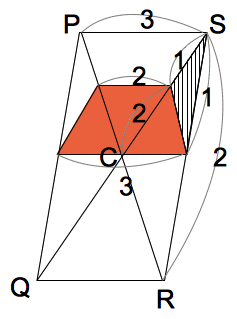
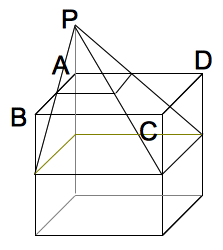
(1)�@���̗����̂_A,B,C��ʂ镽�ʂŐ�AD���܂ޑ��̗���
���c���܂��B
���̂Ƃ�����ɂ���u���b�N�̂Ȃ��ڂ�
�}�Q�ɏ������݂Ȃ����B
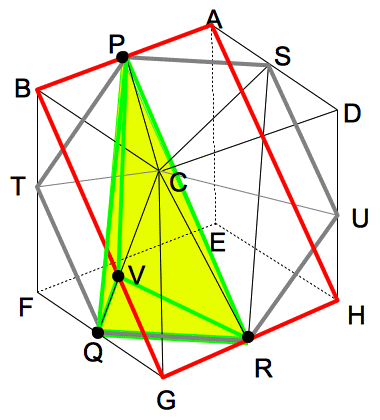
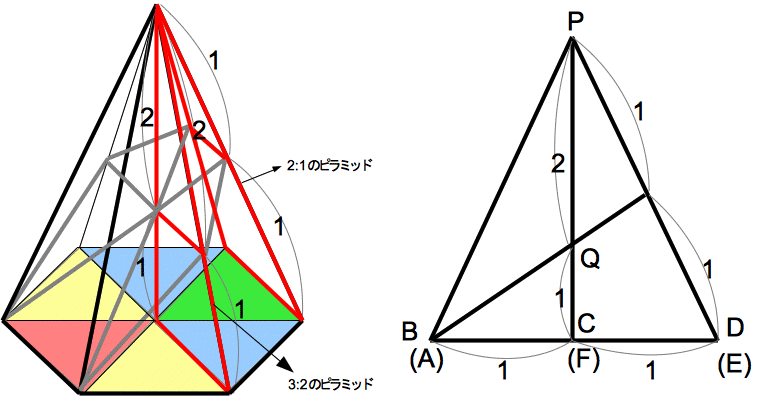
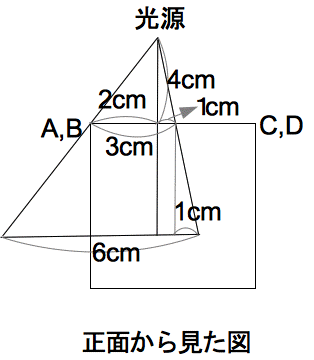
(2)�@�}�Q�̗��̂������
D,B,E ��ʂ镽�ʂŐ�AC���܂�
���̂��c���܂��B���̂Ƃ��A����ɂ���u���b�N�̂Ȃ��ڂ�}�R
�ɏ������݂Ȃ����B
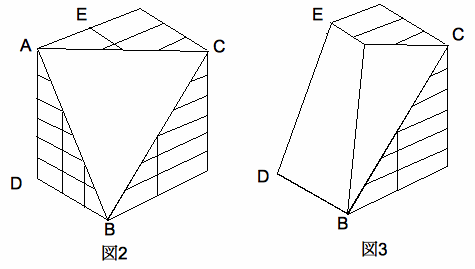
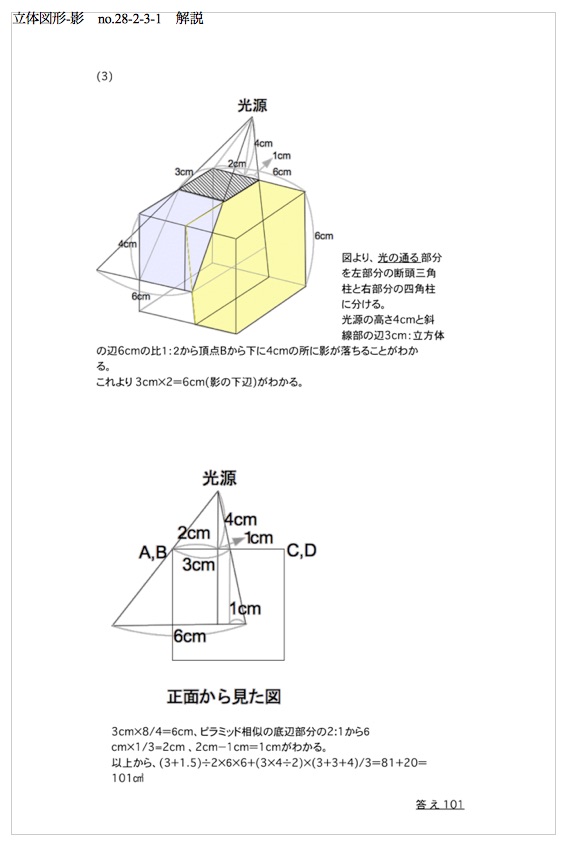
(3) �@�}�R�̗��̂́���
�̃u���b�N�łł��Ă��܂��B���̂����A���Ƃ̒����̂̌`�������u���b�N��
�S���Ł��� ����܂��B
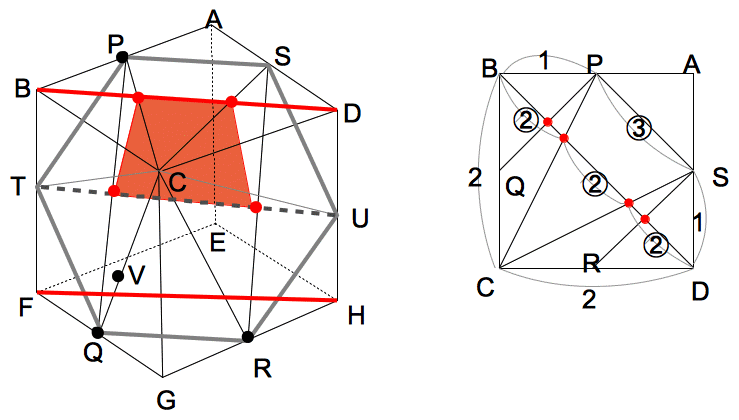
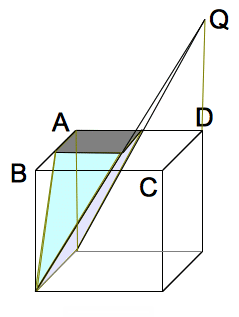
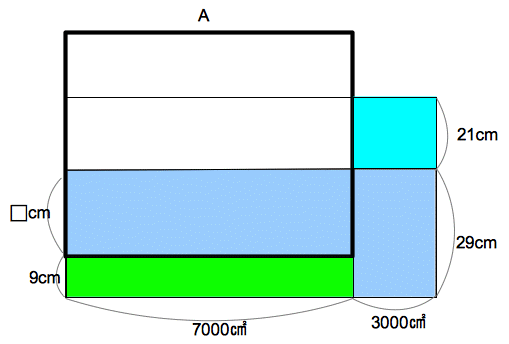
(4)�@�}�R�̗��̂Ɋ܂܂��u���b�N�̂����A�̐ς��ł����������̂��l���� ���B���̃u���b�N
�̑̐ς����߂Ȃ����B
�����@�@�@�@�@㎤






 [���]�@�@�ӂ̒�����1cm,2cm,3cm�̒����̂̌`�������A���g�̋l��
[���]�@�@�ӂ̒�����1cm,2cm,3cm�̒����̂̌`�������A���g�̋l��