プロ家庭教師、尾関が受験算数の核心的問題を紹介します。
カ タラン数
 カ
タラン数とは? カ
タラン数とは?
数学者カタランの発見した数で、次の式で求めることができます。
(2n!)÷{ (n+1)!×n!
} !は階乗ですが、小学生に教えるときは「びっくり」と読んでいます。例えば、「3びっくり」=3!=3×2×1=6ですね。
n=0、1、2、3、4、5、6、7、・・・のとき、それぞれのカタラン数は、1、1、2、5、14、
42,132,429、・・・
最難関中学、超難関中学でよく出題されますが、これを知らなければ時間内で解くのは無理では?という問題も見かけま
す。
そんなカタラン数ですが、どんな問題に応用されているのか、いくつか例をあげてみます。カタラン数を使うということ
に気がつかなけれ ば意 味が ありませんので・・・。
問題1
たし算は二つの数から一つの数を求める計算で、三つ以上の数をたすときには、二つの数のたし算をくり返していくこと
になります。例え ば 1+2+3や1+2+
3+4を、カッコを用いて二つの数のたし算で書き表す方法は、次のようにそれぞれ二通り、五通りあります。
1+(2+3)、(1+2)+3・・・二通り
1+(2+(3+4))、1+((2+3)+4)、(1+2)+(3+4)、(1+(2+3))+4、
((1+2)+3)+4・・・ 五通 り
(注意) 1+(3+2)のように、たす数を並べ替えることは考えません。
このような式を完全式と呼ぶことにします。次のような式は完全式ではありません。
1+2+3、1+(2+3)+4 、(1+2+3)+4 (三つをたしている)
1+2+3+4 (四つをたしている)
(1) 1+2+3+4+5 には何通りの完全式がありますか。
(2) 1+2+3+4+5+6には何通りの完全式がありますか。
問題1の解説
(1) ◆2 個の数の和のとき・・・1通り
◆3個の
数の和のとき・・・2 通り
◆4個の数の和のとき・・・4個の数をとりあえず、(1 個、3個)(2個、2個)(3個、1個)と分けて、2個の数の和の1通りと3個の
数の和の2 通りをあてはめて、2+1+2=5通り
◆5個の数の和のとき・・・5個の数をとりあ えず、(1個、4個)(2個、3個)(3個、2個)(4
個、1個)と分けて、同様にあてはめると5+2+2+5=14通り となる。
答え 14通り
(2) 6個の数をとりあえず、(1個、5個)(2個、4個)(3個、3個)(4個、2個)(5個、1
個)と分けて、同様にあてはめると、
14+5+2×2+5+14=42通り
答 え 42通り
考察
二分木やカタラン数と呼ばれる数列です。
1,2,5,14,42,132,429,1430,4862,16796という風に急激に増加してゆきます。
カタラン数は次の式で定義されています。
Cn= (2n)!/(n+1)!n! !は階乗、例えば、3!= 3×2×1 ですね。
「将来の大学受験に備えて」という事でもないと思いますが、数学の考え方をヒントにした出題はこれからも増
えることでしょう。
問題2
4チームがトーナメントで試合を行い優勝チームを決めます。それには3試合が必要ですが、試合のやり方は何通りあり
ますか。
問題2の解説
• A,Bの2チームしかないときは、もちろん1通り。
• A,B,Cの3チームでトーナメントをするときは、
A対B・・・1試合目、その勝者対C・・・2試合目、このこ
とを、( (AB)C)と表す。
B対C・・・1試合目、その勝者対A・・・2試合目、このことを、(A(BC)を表す。
以上2通りある。
• A,B,C,Dの4チームでトーナメントをするときは、
(((AB)C)D)、((A(BC))D)、((AB)
(CD))、 (A((BC)D))、(A(B(CD))) の 5通りある。
答え 5通り
問題3
表の空らんに1から8までの数字を順に入れてゆくとき、上の段の数字が下の段の数字より小さく、左のらんの数字が右
のらんの数字より 小さ くな るようにします。何通りの入れ方がありますか。
解説
4列のときは、このような入れ方ですが、1列のときは
の1通りあり、2列のときは、左上の1と右下の4は決定なので、
の2通りあり、3列のときも同様に
の5通りある。場合の数が、1、2、5となっているのでカタラン数を予測して、次のオオカミとヒツジ解法で4列の場合を求める。
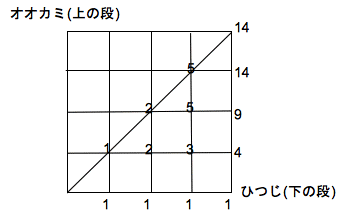
上の段に数字を入れることを、右に1区間進むことに対応させ、下の段に数字を入れることを、上に1区間進むことに対
応させている。
答え 14通り
(別解)
計算でやるには、ガウス公式のように、上下で逆に数をならべて、
1 1 2 5
5 2 1 1
上下に並んだの数の積をすべてたしあわせて、1×5+1×2+2×1+5×1=14通りとなります。
 考 察 考 察
このようにいろいろな場面で登場するカタラン数ですが、「2つの数の和や積」、「1対1の試合」、「上段と下段」、
「オオカミとヒツ ジ」、 「円周上の2点を交わらないよう結ぶ」といった、1対になっている条件付き問 題 で、場合の数
が、1、2、5・・・と増加して行きます。
カタラン数の問題は、最難関校ではよく見かけます
|

カ タラン数とは?
考 察