儂乕儉 |
壠掚嫵巘 |
Zoom庼嬈 |
嶼悢掕棟廤 |
撳偺嶼悢 |
棟壢掕棟廤 |
偍 怽偟崬傒 |
嫵嵽 堦棗 |
岞幃 廤 |
惣 崙弰楃 |
拞 寴乣擄娭峑岦偗zoom庼嬈
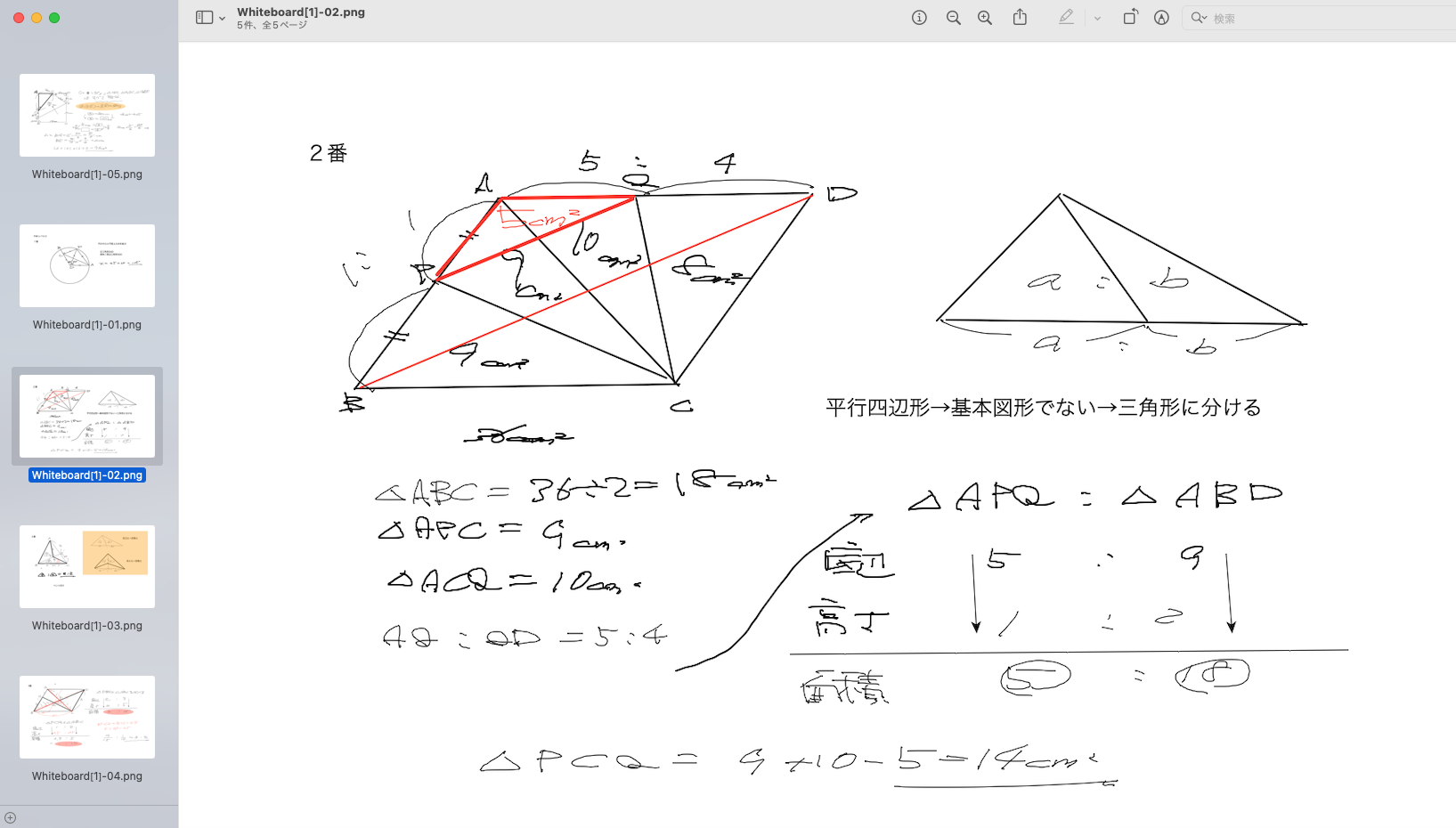
撳拞妛28擭搙侾擔栚偺俋斣 娙扨側栤戣偱偡偑丄尒棊偲偟傗偡偄晹暘偑偁傝傑偡丅 乮栤戣) 塃偺恾偺傛偆側捈妏嶰妏宍ABC偑偁傝傑偡丅偙偺捈妏嶰妏宍偑幬慄晹暘偺奜懁傪丄嘆偺忬懺偐傜栴報偺曽岦偵偡傋 傞偙 偲側偔揮偑偭偰丄嘇偺忬懺傑偱堏摦偟傑偡丅偙偺偲偒丄曈AB偑捠夁偡傞晹暘偺柺愊偼 仩㎠ 偱偡丅 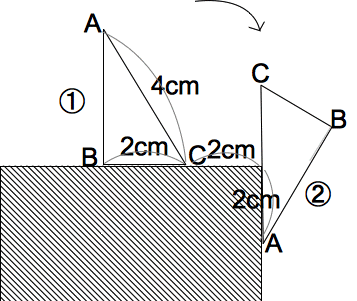 乮夝愢乯 壓恾偺傛偆偵丄曈AB偲夞揮偺拞怱(挿曽宍偺塃忋妏)偺嵟抁嫍棧偼愒偄悅慄偲側傝丄偦偺奜懁偑捠夁晹暘偲側傞丅 惵偄 晹暘偼崌傢偣傞偲傕偲偺捈妏嶰妏宍ABC偺柺愊偲摨偠偵側傞偺偱丄憡嶦偝傟傞丅 捈妏嶰妏宍偲偍偆偓宍偐傜偱偒偨慡懱偺柺愊偐傜丄撪晹偺捠夁偟側偄晹暘傪堷偔偲 16兾/3亄4兾/4亅4兾/3亅兾/4亖14.915  摎 偊丂14.915
撳拞妛28擭搙侾擔栚11斣 惓曽宍偺柺愊傪巊偭偨暯曽悢偺埖偄偲棫懱偺愗抐傪巚偄偮偔昁梫偑偁傝傑偡丅 巐妏偡偄K- AIGJ 偺掙柺愊傪嶰妏宍AKG偲峫偊傞偲丄惓曽宍ABCD偺懳妏慄偺挿偝仩cm偑偙偺棫懱偺崅偝偺榓偲側傞偺偱丄 偦偺懱愊偼丄(3cm亊仩cm亐2)亊仩cm亐3亖仩亊仩亐2 偲側傞丅 偲偙傠偱惓曽宍ABCD偺柺愊偼丄仩亊仩亐2亖36㎠側偺偱丄仩亊仩亖72偲側傝丄 仩亊仩亐2亖72亐2亖36 ㎤偱偁傞丅 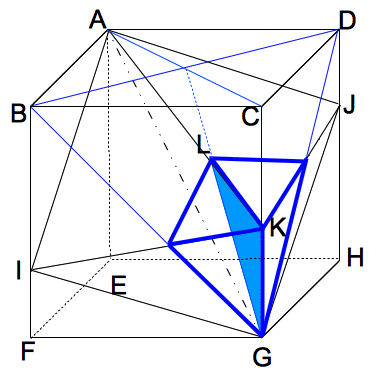 師偵揰K傪娷傓棫懱偼恾偺嶰妏宍KGL傪掙柺偲偟偰崅偝偺榓傪偐偗偰媮傔傟偽傛 偄偺偱丄墶偐傜尒偨恾傛傝丄捀揰L偐傜掙曈KG傑偱偺挿偝偼丄仩亊2/(3亄1亄2)cm偲側 傝丄 忋偐傜尒偨恾傛傝丄揰K傪娷傓棫懱偺崅偝偺榓偼丄恾偺傛偆偵寁嶼偱偒傞丅 傛偭偰丄懱愊偼丄{俁亊(仩亊2/(3亄1亄2)亐2}亊(3/14亄3/10)亊仩亐3 亖3/35亊仩亊仩亖3/35亊72亖216/35㎤偱偁傞丅 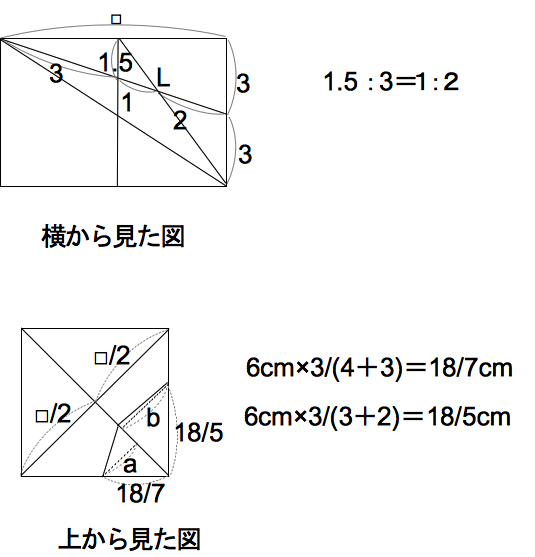 摎偊丂嘆 36 嘇 216/35
|