中学受験、円と 角       

中 学受験プロ家庭教師のペー ジへ

応用公式10

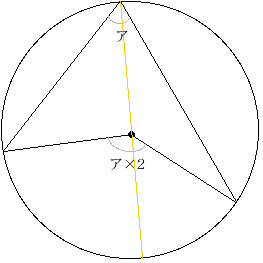
角の頂点が、円の中心にある角を中心角、円周上にある角を円周角 といいます。

円周角＝中心角÷２　となります。

　黄 色の線の両側で、この三角形の外角の定理を使うと、この関係が理解できるでしょう。三角形の外角の定理・・・「一つの外角 は、それにとなりあわない内角の和に等しい。」

(問い)

次の図のような中心角が 100°のおうぎ形OABがありま す。直線ABで、円周の部分を折り曲げたとき、その円周の部分上の点Pが点Qにうつりました。角アの大きさを求めなさい。

(清 風南海)

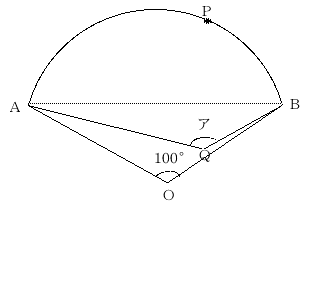
解答 　APとBPをを結ぶ。角Pは円周角となるので、中心角O＝360°ー100°＝260°の半分となる。260°÷2＝130°　

考察　公式を使わない場合は、四角形AOBPの内角の和より、内 角Aと内角Pと内角Bの和は

360°ー100°＝260°　

三角形AOPと三角形BOPは二等辺三角形だから、四角形 AOBPの内角Aと内角Pと内角Bの 和は、三角形AOPの内角Pと三角形BOPの内角Pの和の2倍になる。よって、四角形AOBPの内角Pは

260°÷2＝130°　となり、これが、折り曲げた後の角アに 等しい。　　130°　

算数定理公式集へ