中学受験、折り紙
プロ家庭教師のページへ
次の図でAB+BC=12cm、ED+DC=7cm、直角三角形BCD=10のとき、五角形ABCDEの面積を求めなさい。
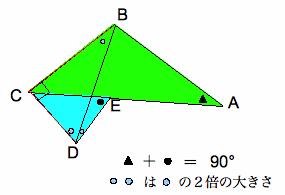
解説
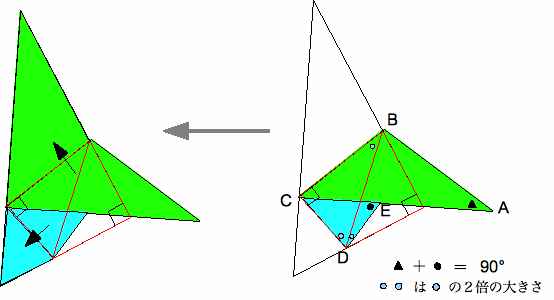
このように、緑と青の三角形をそれぞれ上図のように対称に移動する。さらに赤
い線の三角形がBDについて線対称となるの で、求める面積は、黒い直角三角形の面積 から赤い三角形2個分の20をひけばよい。
底辺と高さは辺ABと辺CDを対称に移動してまっすぐな7cm、12cmとなるので、
7×12÷2−20=22
考察
赤い三角形の合同は、180°の角Dと直角三角形BCDの内角の和180°より、180−(90−青丸)−青丸2個=90−青丸
となり、その結果辺BDと
その両端の角が等しくなります(数学では直接、斜辺と1鋭角相等です)。赤い三角形の直角の頂点は特に辺AC上にあるわけではあ
りません。「くるくる三角
形」の最高峰といえるような問題ですが、ちょうちょの羽がひらひらするようなイメージですので、「ひらひら三角形」とでも名付け
ましょうか。元ネタは単な る1枚の直角三角形の折り紙なのですが、折鶴からもとの展開図を想像するのは簡単ではありません。