中学受験、 みちのりの差が比例す る    

プロ家庭教師の ページへ  

　AさんとBさんはP地を同時に出発してQ地に向かいましたが、AさんがQ地を 折り返してP地にもどる途中、Q地から300ｍはなれた所で、Bさんとはじめて出会いました。AさんがP地にもどったときB さんはP地に向かってP地から 1125ｍはなれた所を歩いていました。AさんとBさんの速さの比を求めなさい。

解説　

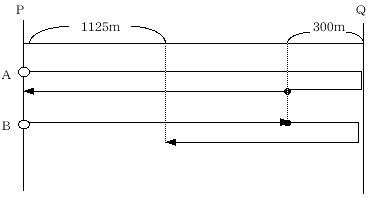
　1回めの出会いでAさんとBさんは　300ｍ×2＝600ｍ　の差 がついた。Aの1往復では　 1125ｍの差がついた。

600：1125＝8：15　　15−8＝７　　8：7　となり　こ の比は　1回めの出会いにか かった時間とその後AさんがP地にもどるまでの時間の比に等しく、言いかえれば1回めの出会いまでに進んだAさんとBさんのみち のりの比に等しい。

これはそのまま速さの比に等しいので　　　答え　8：7

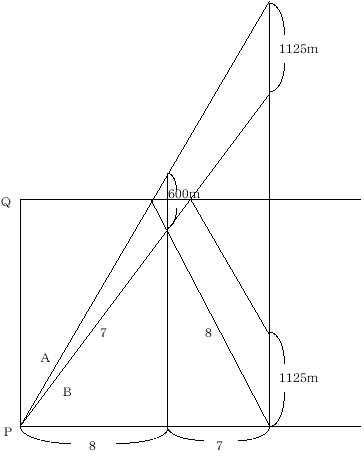
別解として、ダイヤグラムでは、次のようになる。

ダイヤグラムを線対称に折り返して、三角形の相似から　 600：1125＝8：15　15ー8＝7 より　時間の比＝速さの比の逆比＝8：7　となる。

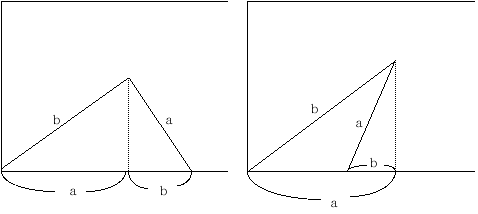
　ダイヤグラムよく使われる三角形ですが、みちのり一定 の時、時間の比は速さの比の逆比になります。

線分図では、線分の同じ長さの部分を比較して時間の比を算出します。「三角形の水平切り」と覚えておき ましょう。

ダイヤグラムよく使われる三角形には他に「三角形の垂直切り」があります。 線分図の線分の同じ時間の部分を比較

して道のりの比などを算出します。こちらは皆さん普通に使っています ね。

算数定理公式集へ