[4]　図のように、面積が16㎠の正方形ABCDの各辺の上に4点P,Q,R,Sをとります。三角形ABP、三角形CQP、三 角形 DQR、三角形ASR の面積はすべて2㎠で、APとRSの交わる点をTとします。このとき、次の問いに答えなさい。


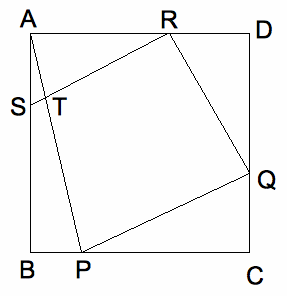
(1)　ASの長さは何cmですか。
(2)　(ATの長さ)：(TPの長さ)　を、最も簡単な整数の比で表しなさい。
(3)　(RTの長さ)：(TSの長さ)　を、 最も簡単な整数の 比で表しなさい。
(4)　四角形PQRTの面積は何㎠ですか。






＜解説＞
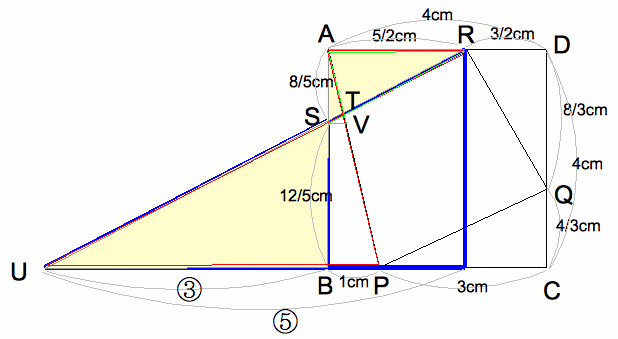
(1)　１辺4cmの正方形である。すべての面積が２㎠とあるので、三角形ABPで、底辺BPを逆算すると、 ２×２÷４＝１cm。よってPC＝４−１＝３cmとなる。三角形PCQにおいて、同様に高さを逆算して、 CQ＝２×２÷３＝4/3cmとなる。同じことを繰り返して、DQ＝4−4/3＝8/3cm、DR＝4÷8 /3＝3/2cm、AR＝4−3/2＝5/2cm、よってAS＝4÷5/2＝8/5cm

(2)　 SB＝4−8/5＝12/5cm 　よって、12/5：4＝3：5　　図の青いピラミッドより、⑤ー③＝②＝4cmー 3/2cm＝5/2cmよって、③＝5/2×3/2＝15/4cm　これよりUP＝15/4＋1＝19/4cmとなる。図の赤い ピラ ミッドよ り、AT：TP＝5/2：19/4＝10：19　である。




(3)　ピラミッドABPより、SV＝1cm÷5×2＝2/5cmである。緑のチョウチョより、5/2：2 /5＝25：4＝RT：TS


(4)　2㎠の４つの三角形を全部たすと、三角形ASTの部分が重なってしまう。(3)の比より、三角形AST＝2㎠÷ (25＋4)×4＝8/29㎠である。よって、四角形PQRT＝16㎠−2㎠×4＋8/29㎠＝240/29㎠　である。









[5]　1か ら20までの数が1つずつ書かれた20枚のカードがあります。この中から1枚目を取り出し、それをもとにもどさないで2枚目を取り出 します。そして1枚目 と2枚目のカードの数の和を計算します。このとき、次の問いに答えなさい。


(1)　 和が10になる取り出し方は何通りありますか。
(2)　和が30になる取り出し方は何通りありますか。
(3)　 取り出し方が最も多いのは、和がいくつのときですか。
(4)　 和が11以上31以下になる取り出し方は全部で何通り ありますか。
　
　

＜解説＞
(1)　 (1枚目、2枚目)と並べると、(1,9)　 (2,8)・・・・(9,1)となるが、(4,4)は含まないので、9−1＝８通りある。

(2)　 同様に、(10,20)　(11,19)・・・ (20,11) のうち(15,15)は含まないので、11−1＝10通り

(3)　

和	10	11	・・・	19	20	21	22	23	・・・	30	31
通り	8	10		18	18	20	18	18		10	10

表より、 和が21のときで、20通りである。
(4)　和が12〜30の偶 数のとき、場合の数が1通りずつ減 るので、減らない と考えたときの連続する整数の和からそれらを引けばよい。
10＋11＋12＋・・・＋20＋19＋・・・ 11＋10−10＝ (10＋20)×11÷2＋(19＋10)×10÷2−10＝300通り