洛南中学2010年 算数 中学 受験・算 数・プロ家庭 教師のページへ
[1] 次の□にあてはまる数を答えなさい。
(1) 1+8+15+22+29+36+43=□
(2) 123+456+231+564+312+645=□
(3) 2×(9.2+2.7)+3×(5.5−1.8)−4× (2.3−1.5)−5×(3.3+1.2)=□
(4) 1.76×8.25−1.32×1.65−0.44×2.75−0.22×1.1=□
(5) 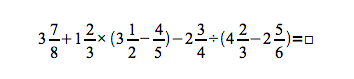
(6) 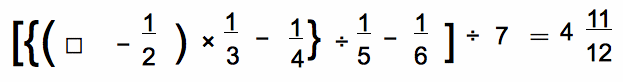
<解答>
[1] (1) 154 (2) 2331 (3) 9.2 (4) 10.89 (5) 55/8 (6) 22
[2] 次の問いに答えなさい。
(1) 次の図のおうぎ形において、(弧ABの長さ):(弧CDの長さ)=5:3、角BOCの大きさは24°、角DOAの大きさは 144°です。角アの大きさは何度ですか。 ( 度)

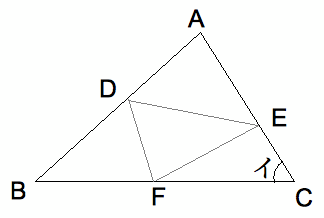
(2) 次の図の三角形ABCの紙をDEを折り目として折ると、AがBC上のFになりました。次にDFを折り目として折ると、BがAC上のE になりまし た。このとき、角イの大きさは何度ですか。 ( 度)
<解答>
[2] (1)

144:24=6:1 5:3と1:6の比を最小公倍数で合成すればよい。5+3=1+6 より、8=7→56 にそろえる。ア=5×7−1×8=27 8=24°より、 24÷8×27=81°
答え 81°
(2)
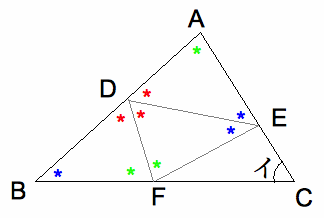
三角形DEFで赤+青+緑=180°だから、三角形ABCの内角の和より角イは赤の角に等しい。 赤=180°÷3=60°である。
答え 60°
(3) 次の図は、円柱の形をした容器の中に、円すいの形をした容器を、底面がともに水平になるように差し込んだものです。ウはいくらです か。 ( cm)

<解答>
(3)
円すいの高さは5cm、差し込まれた部分の高さは5−1=4cm、よって5:4のピラミッドの相似より、 ウ=3cm÷4×5=3.75cm
答え 3.75cm
(4) 次の図のように、正方形ABCDを点Dを中心として60°回転させると、正方形A'B'C'D'となりました。斜線部の面積 は、黒い部分 の面積の何倍ですか。
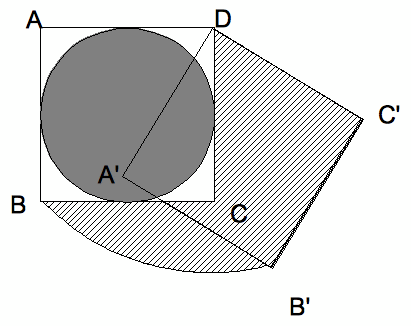
<解説>
(4)
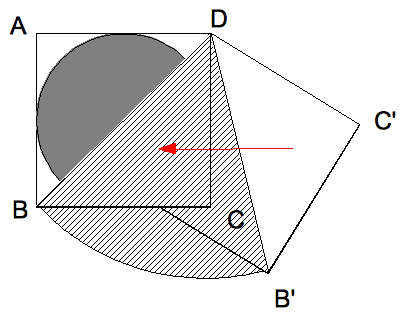
左のように、斜線部の三角形B'C'D'を三角形BCDに移動させると、おうぎ形BB'Dの面積と等しくなる。その半径×半径は 正方形 ABCDの面積の2倍である。黒い円の半径を1とすると正方形の面積は2×2=4となり、このときおうぎ形BB'Dの面積は、 4×2倍×3.14÷6=8÷6×3.14である。
よって、(8÷6×3.14)÷(1×1×3.14)=4/3倍となる。
答え
(5) 次の図の網目部分の図形を軸ABで回転したときにできる立体の体積は、黒い部分 の図形を軸ABで回転したときにできる立体の体積の何倍ですか。ただし、各マス目は正方形です。

<解説>
(5)
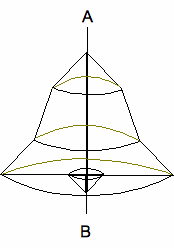
小さな黒い部分を回転してできる円すいの体積は、半径×半径×高 さ=1×1×1=1に比例する。円すい 台の体積の公式は、上底面積(A)×下底面積(B)から2乗を取った数をCとすると、(A+B+C)×高 さ÷3と なるので、斜線部の1段目から3段目までの体積合計は、2×2×2+ (2×2+3×3+2×3)×3+ (3×3+5×5+3×5)×2=163に比例する。
答え 163倍
[3] 図の四角形ABCD は長方形です。このとき、次の問いに答えなさい。

(1) (BEの長さ):(EFの長さ):(FGの長さ)を、最も簡単な整数の比で表しなさい。
(2) 黒い部分の面積は何㎠ですか。( ㎠)
(3) 斜線部の面積は何㎠ですか。( ㎠)
<解説>
(1) 下の図で、黄色い三角形の相似から、4cm:6cm=2:3=BE:FGとなり、緑の三角形の相似から、BE:EF=3:1 となる。よって、 BE:EF:FG=3:1:2 答え 3:1:2
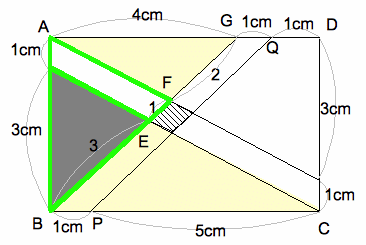
(2) BE:EG=3:3=1:1だから、黒い三角形の高さは4cm÷2=2cmとなるので、 3×2÷2=3 ㎠
答え 3㎠
(3) 平行四辺形BPQG=1cm×4cm=4㎠であり。その底辺をBG と見ると、EF:BG=1:(3+1+2)=1:6なので、斜線部の三角形の面積は、4㎠÷6=2/3㎠
答え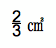
[4] ビーカーAにはある濃度の食塩水が240g、ビーカーBには濃度が5%の食塩水
がいくらか入っています。いま、AからBへ90g移すと、ビーカーBの食塩水の濃度は5.6%になりました。さらに、Aの残りの食塩
水をすべて移すと、B の食塩水の濃度は6.1%になりました。このとき、次の問いに答えなさい。
(1) Aに入っていた食塩水の濃度は何%ですか。( %)
(2) Bに入っていた5%の食塩水は何g ですか。( g)
<解説>
(1)
 (5.6−5):(6.1−5)=0.6:1.1=6:11が
右回りのモーメントの比であり、これと左回りのモーメントがつ りあっているので、(6÷90):(11÷240)=16:11が
わかる。16−11=5が
6.1−5.6=0.5%にあたる ので、 0.5%÷5×16=1.6%
(5.6−5):(6.1−5)=0.6:1.1=6:11が
右回りのモーメントの比であり、これと左回りのモーメントがつ りあっているので、(6÷90):(11÷240)=16:11が
わかる。16−11=5が
6.1−5.6=0.5%にあたる ので、 0.5%÷5×16=1.6%
5.6%+1.6%=7.2% がAの濃度となる。
答 え 7.2%
(2) 90×(7.2−5.6)=B×(5.6−5) より B=240g
答え 240g
[5] 半径1cmの円を、長方形の中に図の(ア),(イ)の2通りの方法でできるだけ多くならべていくことを考えます。
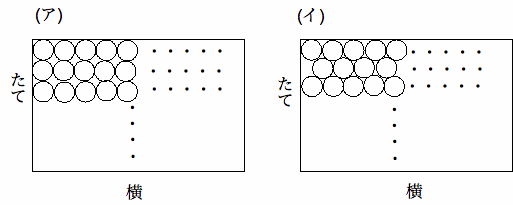
次の長方形の中に円をならべていくとき、(ア)と(イ)のならべかたでは、どちらの方が何個多くならべることができますか。ただし、 1辺の長さが1cmの 正三角形の高さは0.87cmとします。
(1) たて8cm、横30cmの長方形 ( の方が 個多い)
(2) 縦20cm,横30cmの長方形 ( の方が 個多い)
<解説>
(1) アでは、(8cm÷2cm)×(30cm÷2cm)=60個ならび、イでは、 1.74cm×3+2cm=7.22cmより3+1=4行ならぶので、15個×2+14 個×2=58個ならぶ。答え アの方が2個多い
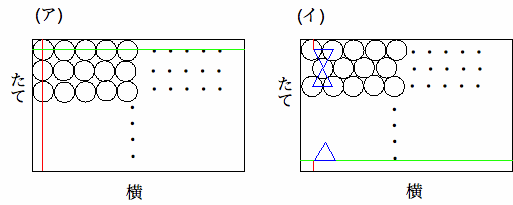
(2) アでは、10×15=150個ならび、イでは、1.74cm×10+2cm=19.4cmより 10+1=11行ならぶの で、(15個+14個)×5+15個=160個ならぶ。答え イの方が10個多い
[6] 図のように、周の長さが1200mの正六角形の形をした池があり、BE間には、まっすぐな橋がかかっています。太郎君はBを
出発して毎分100m の速さでEまでこの橋を渡ります。次郎君はAを出発してL
との間を、花子さんはAを出発してMとの間をそれぞれ一定の速さのボートでまっすぐ往復します。3人は同時に出発し、次郎君と花子さ
んは、同時にAに戻る
まで休むことなく往復し続けました。次郎君と花子さんがそれぞれはじめて橋の下にきたとき、その真上に太郎君がいました。L,Mはそ
れぞれCD,DEの真 中の点です。このとき、次の問いに答えなさい。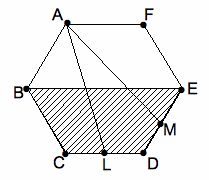
(1) 次郎君がはじめて橋の下にくるのは、出発してから何分何秒後ですか。
( 分 秒後)
(2) (次郎君のボートの速さ):(花子さんのボートの速さ)を、最も簡単な整数の比で表しなさい。
(次郎の速さ):(花子の速さ) ( : )
(3) 次郎君と花子さんが同時にAに戻るのは出発してから何分後ですか。また、この間2人がともに斜線部の範囲にいるのは何分何秒 間ですか。
( 分後) ( 分 秒間)
<解説>
(1)  赤いピラミッドの相似から、太郎は
300m÷2=150mを毎分 100mで進むので、 150÷100=1.5分後に次郎が橋の下にいる。
赤いピラミッドの相似から、太郎は
300m÷2=150mを毎分 100mで進むので、 150÷100=1.5分後に次郎が橋の下にいる。
答え 1分30秒後
(2) 青いピラミッドの相似から、400m÷(1+2)=400/3m、400m−400/3m=800/3mを太 郎は進むので、800 /3÷100=8/3分後に花子が橋の下にいる。ところでAL=AMなので、次郎はAL間を1.5 分×2==3分で、花子は AM間を8/3分÷2×3=4分で進み、これらの逆比が速さの比なので、4:3である。
答え 4:3
(3) 次郎は、1.5分×4=6分ごと、花子は、(8/3分×3/2)×2=8分ごとにAに もどるので、6と8の 最小公倍数の24分後に同時にAにもどる。
次郎は、斜線部に1.5~4.5分、7.5~10.5分、13.5~16.5分、19.5~22.5分の間にいる。花子は斜線部に、 8/3~16/3分、 32/3~40/3分、56/3~64/3分の間にいる。同時にいるのは、(4.5−8/3)+(64/3−19.5)=11/3分 すなわち、3分40秒 間いることになる。
答え 24分後 3分40秒間
[7] 1,1+2,1+2+3,1+2+3+4,1+2+3+4+5・・・・のそれぞ れの数を6で割った余りを並べると、
1、3、0、4、3、・・・
という数の列になります。この数の列について、次の問いに答えなさい。
(1)22番目の数は何ですか。( )
(2) 1番目から22番目までの数をすべてたすといくらです か。 ( )
(3) 22個目の0は、全体の何番目の数ですか。( )
(4) 1番目から2010番目までの数をすべてたすといくらですか。( )
<解説>
(1) (1+22)×22÷2=253 253を6で割ると1あまる。 答え 1
(2) 1,3,0,4,3,3,4,0,3,1,0,0の12個の繰り返しになっているので、24番目までの和は 22×2=44で、 23,24番目は0だから、44である。
答え 44
(3) 12個の1周期の中に0は4個ふくまれるので、4個×5+2 個=22 個より、12×5+8=68番目(2個目の0は8番目にあるので)
答え 68番目
(4) 2010÷12=167・・・6より、 22×167+14=3688 答え 3688
[8] 次の、あ〜え にあてはまる数を答えなさい。
あ( ) い( ) う( ) え( )
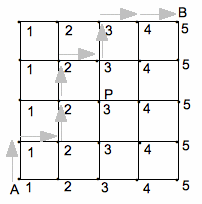
最短経路を選んでAからBまで行きます。Aでまず1点を得て、各交差点で図中の点数を得ながら進んで行き、最後にBで5点を得て、合 計得点を計算します。 例えば、図中の矢印のように進むと、1+1+2+2+2+3+3+4+5を計算して、合計得点は23点となります。
(1) AからPを通ってBまで行く経路の合計点は最高で, ( あ )点となります。
(2) 合計得点が( あ )点となる経路をすべて考えると、全部で( い )通りあります。
(3) 合計得点が偶数となる経路をすべて考えると、全部で( う )通りあります。その( う )通りの経路それぞれの合 計得点の平均は( え )点となります。
<解説>
(1) 1+2+3+3+3+4+5+5+5=31 答え あ=31
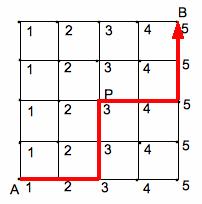
(2) 横方向はどの経路を通っても、1+2+3+4+5=15点なので、たて方向の和が、31−15=16点になる組み合わせを考 えればよい。
1→5の方向の辞書式配列で、1+5+5+5、2+4+5+5、3+3+5+5、3+4+4+5、4+4+4+4、の5通りある。
答え い=5
(3) 横方向の和は15点なので、たて方向の和を奇数にすれば、合計得点を偶数にでき る。
奇数の区間をを1区間だけ通るとき、
1222,1224,1244,1444 ・・・点数はそれぞれ7,9,11,13で4通り
3222,3224,3244,3444・・・点数はそれぞれ9,11,13,15で4通り
5222,5224,5244,5444・・・点数はそれぞれ11,13,15,17で4通り
奇数の区間をを3区間だけ通るとき、
1112,1114・・・点数はそれぞれ5,7で2通り
1132,1134・・・点数はそれぞれ7,9で2通り
1152,1154・・・点数はそれぞれ9,11で2通り
1332,1334・・・点数はそれぞれ9,11で2通り
1352,1354・・・点数はそれぞれ11,13で2通り
1552,1554・・・点数はそれぞれ13,15で2通り
3332,3334・・・点数はそれぞれ11,13で2通り
3352,3354・・・点数はそれぞれ13,15で2通り
3552,3554・・・点数はそれぞれ15,17で2通り
5552,5554・・・点数はそれぞれ17,19で2通り
以上より、全部で32通り、それぞれの和は384点となるので、384÷32=12点、これに横方向の和の 15点を足して、 12+15=27点となる。
答え う=32、え=27