同じ種類の電池と電球、電流計を
用いて実験をしました。電流計をつないでも回路を
流れる電流の強さは、そこを導線でつないだときと変わらないものとします。
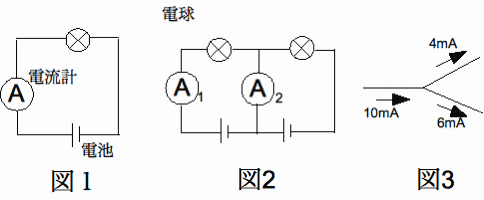
図１のように電球、電流計、電池１個を直列につなぐと、電流計の読みは10mAになりました。この回路で、直列につなぐ電池の個
数を１個ずつ増やして、電
池の個数と電流計の読みとの関係を調べると次の表のようになりました。
| 電池の個数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 電流計の読み(mA) |
0 |
10 |
15 |
19 |
23 |
26 |
29 |
32 |
35 |
38 |
40 |
また図２のように電池２個と電球２個とでできた回路では電流計1の読みが10mA、電流計2の読みが0mA(電流が流れない)でし
た。なお、回路のとちゅ
うで導線がわかれている場合、わかれる点に流れ込む電流の強さの合計と、わかれる点から流れ出す電流の強さの合計は同じになります
(図３の数値は１つの例
です)。
解説
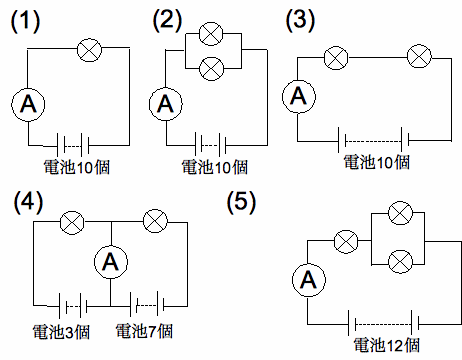
(1)
10個の電池が直列つなぎになっているので、表より40mAの電流が流れる。
(2) 並列つなぎの豆電球の一方をかくした回路と考えて、(1)と同様に
それぞれ
の豆電球に40mAの電流が流れる。よって、電流計には40＋40＝80mAの電流が流れる。
(3) 直
列つなぎの乾電池÷直列つなぎの豆電球＝10個÷2＝5個より、電池5個分の電流が豆電球に流れる。よって、表より26mAの電流が
流れる。
(4) 直列つなぎの乾電池÷直列つなぎの豆電球＝3個÷1＝3個より、表
から
19mAの電流が回路の左部分を流れ、同様に7個÷1＝7個分すなわち32mAの電流が回路の右部分を流れる。図３の例と同じように
考えて、
19mA＋□mA＝32mAのように合流するので、32−19＝13mAの電流が電流計を流れることになる。
答え 13mA
(5) 電球の並列部分の合成抵抗は、電球0.5個分なので、回路全体では 1 個＋0.5個＝1.5個分の合成抵抗となる。直列つなぎの 乾電池÷直列つなぎの 豆電球＝12個÷1.5＝8個より、表から35mAの電流が電流計を流れる。