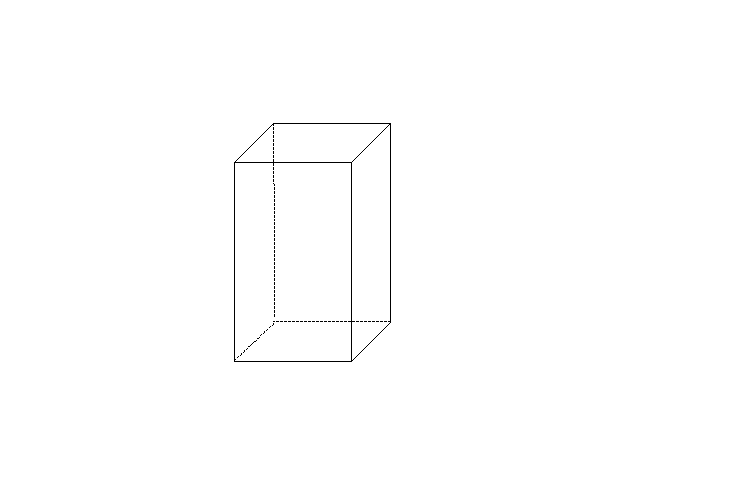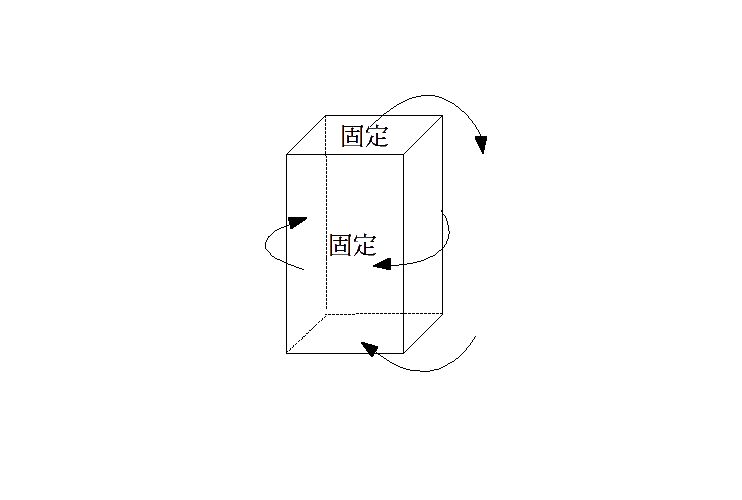中学受験算数ー直方体のぬり分け
次の図のような底面が正方形である直方体の6
つの面をぬりわけることにします。6色すべてを用いてぬり分ける方法は何通りありますか。
また、5色すべてを用いてぬり分ける方法は何通りありますか。
(希学園)
解説
図のようにたて方向と横方向に回転できるので、重なりが起きる。面は底面と側面の2通 りあり、その どちらかに"ある1色”をぬって固 定する。"ある1色” を上の底面にぬったとき、その対面は5通り のぬり方 があり、つぎに正面の側面に"他のある1 色”をぬり固定すると、残り3色のぬりかた は3×2×1=6通りある。よって、5×6=30通 り。
ま た"ある1色”を正面の側面にぬったとき、 他の側面は5×4×3=60通りあり、つぎ に底面の1つに"他のある1色”をぬり固定すると、残り 1色のぬり方は1通り。よって、 60×1=60通り。
以 上から、 30+60=90通りとなる。
答え 90通り
次 に5色の場合は、ぬる場所が1カ所不足なので、同色をぬ る所を決める必要がある。
2つの底面に同色をぬるとき、5通りの色の選び方があり、向かい 合った底面にその色をぬる(回転しても変わらないので1通り)。そ れぞれに対して側面の1つに"ある1色"をぬり固定すると残り3色で3×2×1=6通りのぬり 分けができる。すなち、5×1×3×2×1=30通り。
2つの側面に同色をぬるとき、5 通りの色の選び方があり、向かい 合った側面にその色をぬる(回転しても変わらないので1通り)。それ以外の面の1つに"ある1色"をぬり固定すると残り3色でその対面には 3通 りのぬり方がある。次に残り2面のうちの1つの面に残 りの"ある1色をぬり固定する とその対面には1通りのぬり方があ る。すなわち、 5×1×3×1=15通り。よって、30+15= 45通りとなる。
答え 45通り
考察
もし底面が長方形で、上下、左右、前後それぞれ合同な3種類の長方形(A,B,Cとする)でできている直方体の場合 は、どうでしょう。
" ある1色”をAにぬると すると対面A'のぬり方は5通りあり、残り4色のうち1色をぬる方法はB、Cの長方形のうち1つだから2通りあり、その対面 のぬり方は3通りである。残り 2面をぬる方法は2通りあるので、3×5×2×3×2=180通りです。” 残り2面”はその前の2回の固定によってもう動かないので、2×1=2通りです。
面が何種類あるかがポイントです。合同な4つの側面をぬる場合は円順列で一気にできますが、2面ずつ合同なときは、 対面のうち1面を固定して1回ずつ計算 します。
少し深い考え方ですのでじっくり考えて下さい。実際にぐるぐる回して、重なる場合をすべて書き出して数え上げ、すべ ての場合の数を割ってもできます。希学 園灘プレミアムの解説はそちらの方のやり方になっています。どちらでやるかは、わかりやすい方を選んで下さい。
算数定理公式 へ