[数学ーメネラウスの定理]
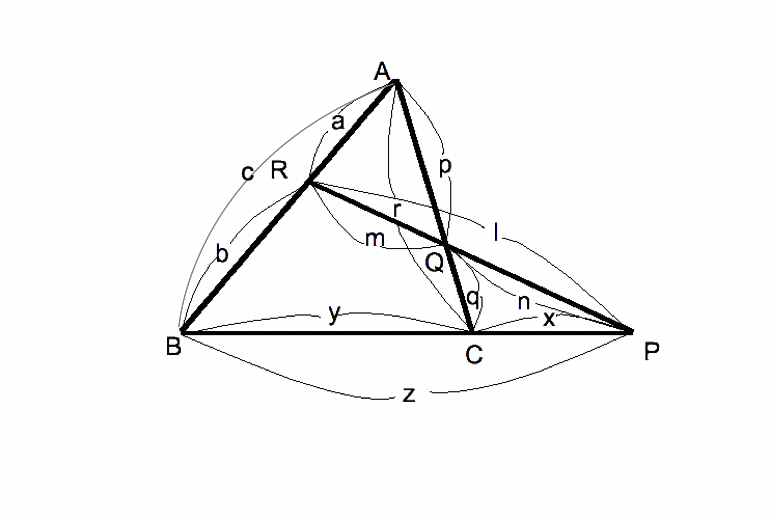
次の図で、z/x・r/p・n/l・a/c＝
１となることをメネラウスの定理を用いて示せ。ただし、AR=a、RB＝b、AB=c、CP＝x、BC=y、BP=z、AQ=p、
CQ=q、AC=r、
PQ=n、RQ=m、PR=l とする。
(洛星中学)
解説
△ABCにメネラウスの定理を用いて、a/b・z/x・q/p＝１が成立する。
また△ARQにおいて同様にして、b/c・r/q・n/l＝１が成立する。
よって、左辺どうしをかけあわせて、a/b・z/x・q/p・b/c・r/q・n/l＝１となる。
約分してならべかえると、a/c・r/p・z/x・n/l＝１
考察
メネラウスの定理は、一般には、内分×外分×内分＝１ですが、この問題のように、外分×外分×外分＝１でも使わ れます。(外分点は奇数個)
チェバの定理は、内分×内分×内分＝１、外分×内分×外分＝１としても使われます。( 外分点は偶数個)
メ ネラウスの定理は「三角形の頂点 を通らない直線が、三角形の三辺またはその 延長上で交わる点」を内分点または外分点として成り立つ定理です。
紀元100年頃に発見された定理だそうです。チェバの定理とともに中学受験でもよく出題されます。