[中学受験算数・場合の数]
9人
から３人ずつの組を３組作る方法は何通りありますか。
解説
9人から3人を選び、残った６人から3人を選べば残り３人は自動的に決まるので、
9C3×6C3＝(９ ×８×７)÷(3×２×1)×(6×５×４)÷(3×２×１)＝1680通りある。
9C3をA グループ、6C3をBグループ、残りをCグループとする と、この問題では組A,B,Cの区別はないので重なりを取り除く必要がある。A,B,Cの順列は3×２×1＝６通りだから、1680÷6 ＝280通りである。
算数では、次の通りです。
はじ
めに１人選んで組を固定します。円順列と同
じ手法です。もちろん９通りのうち誰を選んでも同
じですの
で、１通りと数えましょう。
◎ ◯ ◯ ◯ ◯ ◯ ◯ ◯ ◯
はじめに◎１人を選んで残
り８人からメンバーを2人選ぶと、
７＋６＋５＋４＋３＋２＋１＝28通りある。→◎ ◎ ◎
◯ ◯ ◯ ◯ ◯ ◯となる。
◎ ◎ ◎ ● ◯ ◯ ◯ ◯ ◯ つぎに●１人を選んで残り５人からメンバーを２人選ぶと、
４＋３＋２＋１＝10
通
りある。→◎ ◎ ◎ ● ● ● ◯ ◯ ◯となる。
◎ ◎ ◎ ● ● ● ● ● ● 残り３人は自動的に決定する。
28×10＝280通り
考察
誰が呼んだか「組合せシャワー」です。←日能研でしたか？
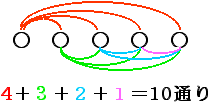
もちろん数学の助けを借りて、5C2で
もいいですよ。←浜学園、希学園方式？
算数VS数学、どっちの勝ち？ 数学は何か偉そうで、そのくせ遠回りして
いるのが
気に入りません。
とりあえず私は割り算がキライなので、独断で算数の勝ち！！