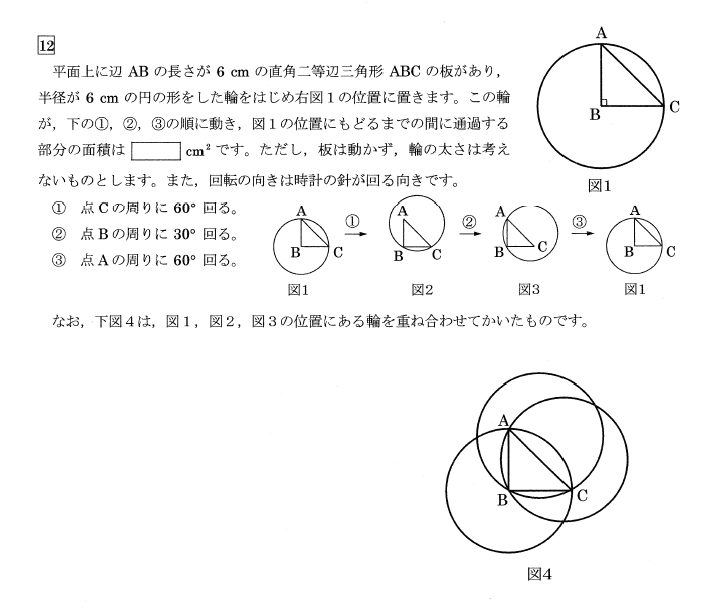
<解説>
(1)
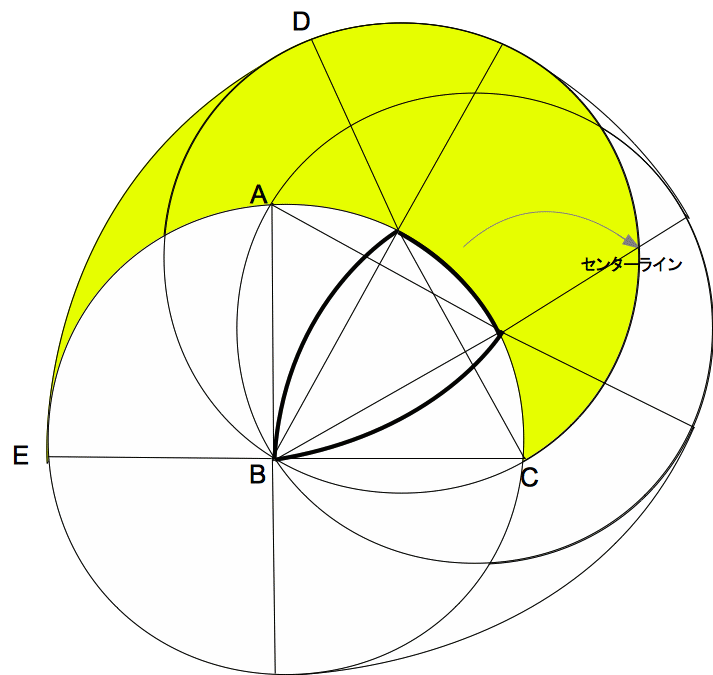
上図で黄色部分は半円を60°時計回りに移動してできた図形なので、おうぎ形CDEに等積変形できる。
下図の緑部分も同様におうぎ形AKLに等積変形できる。

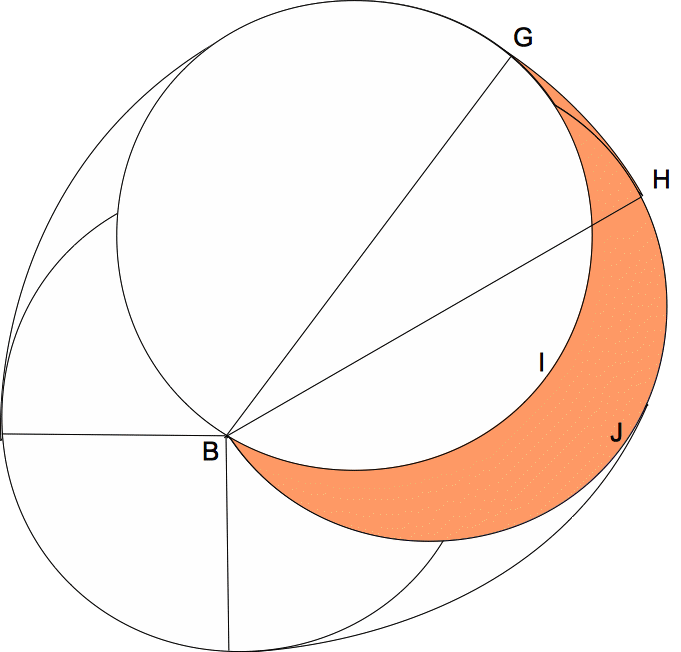
下図の赤部分も半円を時計回りに30°移動してできた図形のなので、おうぎ形BGHに等積変形できる。
以上から、中心角が60+60+30=150°のおうぎ形の面積になるので、 12×12×π×5/12=60π=188.4㎠となる。
答え 1888.4㎠
結果的には、最上部の図にあるように円の中心が動いた後センターラインの長さ×円の直径というお馴染みの形になってしまうようです。
このような問題を私は「遊星歯車問題」と勝手に名付けていますが一つの対処方法として覚えておいてもよいでしょう。