ガウス記号の問題数Xに対して、Xをこえない整数のうち、最も大きいものを[X]で表します。
例えば、[3.3]=3、[4]＝4です。
次の2010個の整数の中に全部で何種類の整数がありますか。
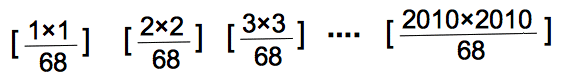
解説
となりあった分子の差が68未満のときは ０から連続する整数が並び（同じ整数が繰り返すこともある)68を越えると[x]の値はすべて１：１対応となる。
35×35−34×34＝69ではじめて 差が68を越える。
x＝34のとき、
[x]＝34×34÷68＝17 なので、0から17までの18種類の整数が現れる。
35×35〜2010×2010までは1：1対応で整数が現れるので、2010−34＝1976種類の整数が現れる。
18＋1976＝1994種類である。
答え 1994種類