[中学受験算数ー場合の数]
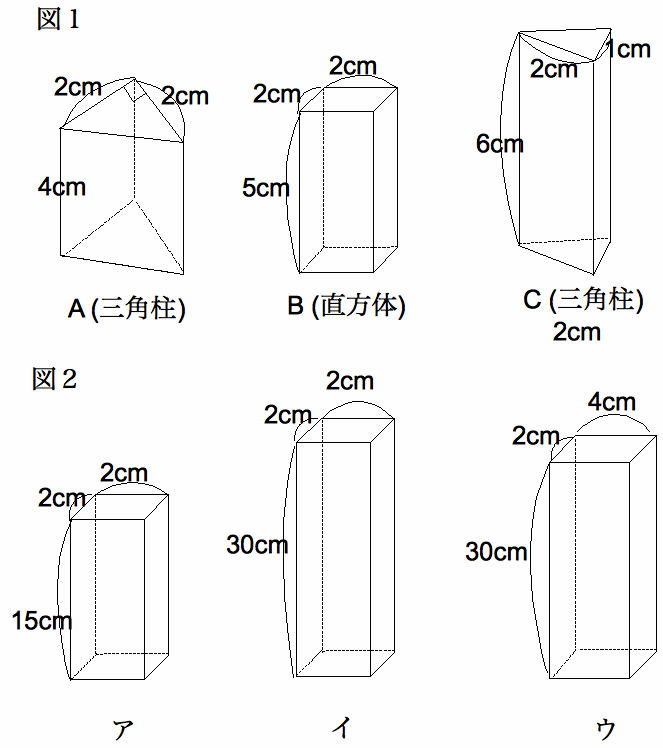
図１のような
積み木A、B、Cがそれぞれたくさんあります。これらをいくつかずつ使い、すき間なくくっつけて、図２のような直方体を作ります。ただ
し、どの積み木も必ず１つは使うものとします。このとき次の問いに答えなさい。
(1) アを作るとき、A、B、Cをそれぞれいくつずつ使えばよいですか。
(Aの個数、Bの個数、Cの個数)の形で答えなさい。
(2) イを作るとき、A、B、Cをそれぞれいくつずつ使えばよいですか。考えられる場合を、すべて(Aの個数、Bの個数、Cの個数)の 形で 答えなさい。
(3) Bをちょうど６個だけ使ってウを作るとき、(Aの個数、Cの個数)の組み合わせは全部で何通りありますか。
(4) ウを作るとき、(Aの個数、Bの個数、Cの個数)の組み合わせは全部で何通りありますか。
(洛南高付属中)
解説(1) 高さは、４＋５＋６＝15cmとなるので、(２、１、４) となる。
(3) 5cm×６＝30cmより、B６個でウをたてに２等分した四角柱が１つできる。次に残り１つを作る。A２個で作った四角柱をA'、C4個で
作った四角柱をC'とする。どちらも底面積が１辺2cmの正方形の正四角柱である。
４cm×３＋６cm×３＝30cm または、4cm×６＋６cm×１＝30cm となるので、(A’、C’)＝(3、3)
、（６、1) すなわち(A、C)＝(6、12)、(12、4) となる。・・・①
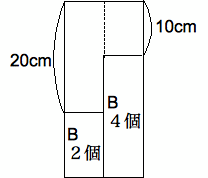
Bを分けて積むとき、下図のように、２個と４ 個に分けて積み(奇数個は積めな い)、上部のすき間は20cm、10cmとなるので、A'とC’で4cm×2＋6cm×２＝20cm積め、 4cm×1＋6cm×1＝10cm が積める。このとき、(A'、C')＝(3、3)すなわち、(A、B)＝(6、12)となる。・・・② よって①②より、(6、 12)、(12、4)の2通りだけとなる。
答え ２通り
(４) 前問より、(A、B、C)＝
(6、6、12)すなわち(A'、B、C')＝(3、6、3)のとき、
B２個と(A'１個＋C'１個)はいれ かえられるので、(A'、B、C')＝(4、4、4) (5、2、5) (2、8、2)
(1、10、1) 。
また、A'3個とC'2個もいれかえられるので、(A'、B、C')＝(6、6、1)ができ、(A'、B、C')＝(4、4、4)
から
(1、4、6) (7、4、2)ができ、(A'、B、C')＝(5、2、5) から(8、2、3) (11、2、1) (2、2、7)
ができる。
次に、(A、B、C)＝(12、6、4)すなわち(A'、B、C')＝(6、6、1)の
とき、B２個と(A'１個＋C'１個)はいれかえられるので、(A'、B、C')＝(7、4、2) (8、2、3) (これらは既
出)。
また、A'3個とC'2個がいれかえられるので、(A'、B、C')＝(3、6、3)(これも既出)。以上から全部で11通りある。
答え 11通り
考察(3)で、②の(A、B)＝(6、12)の場合は「数字のいれかえ」という意味では、①の(A、B)＝(6、12)と同じ結果になる の で、(4)の問いで実際に図形的にあり得るかどうかを確かめる必要はなく、①の場合の数だけでよいことになります。個数の場合の数を聞い ているのであって、積み上げ方の場合の数を聞いているのではないからです。