2021年度　灘中学１日目 [1] 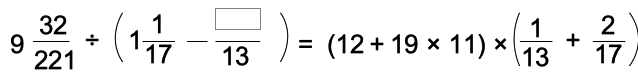    解説：221×43/(13×17)＝43 2021/221÷1/43＝47/221 (18/17−47/221)×13＝(234−47)/17=187/17＝11 答え１１ [2]　3つの容器A,B,Cにあわせて600mLの水が入っています。容器Bの水の 体積は容器Aの水の体積の1.5倍です。 容器Aから容器Bに水を40mL移すと、容器Bの水の体積は容器Cの水の体積の1.4倍になりました。水を移した後 の容器Bの水の体積は mLです。 解説：A＝�A　B＝�B　C= 5︎⃣ 計600mL  とする。 Aから40mLをBに移すと、Bの水は 5︎⃣×1.4＝ 7︎⃣になった。 すなわち、�B＋40＝ 7︎⃣、�D＋ 5︎⃣＝600 が成り立つ。 これより、1︎⃣＝40、7︎⃣＝280となる。 答え　280 [3]　2021の各位の数の和は 2＋0＋2＋1＝5です。このように各位の数の和が５である4桁の整数は、2021を含めて全部で個あります。そしてそれらの整数の中で2021は小さい方か ら数えて番目です。 解説：４桁の整数とあるので、千の位で場合分けする。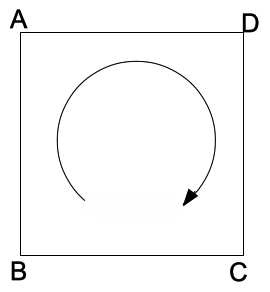 例をあげながら計算をすると ・千の位＝１のとき、｜◯◯◯｜◯→1031   ２本の ｜ と４個の◯の順列なので、6!÷(4!×2!)＝15個 ・千の位＝2のとき、◯｜◯｜◯→2111   ２本の ｜ と3個の◯の順列なので、5!÷(3!×2!)＝10個 ・千の位＝3のとき、◯◯｜｜→3200    ２本の ｜ と2個の◯の順列なので、4!÷(2!×2!)＝6個  ・千の位＝4のとき、◯｜｜→4100    2本の ｜ と1個の◯の順列なので、3個 ・千の位＝5のと き、5000の１個だけ 以上から、15＋10＋6＋3＋1＝35個 答え　 35個 [4]　右の図のような正方形ABCDの辺上を３点P,Q,Rが動きます。点Pは点Bを出発し図の 矢印の向きに、 点Qは点Aを出発し図の矢印の向きに、点R は点Cを出発し図の矢印と反対の向きに動きます。 点Qの動く速さは点Pの動く速さの３倍です。３つの点が 同時に出発し、点Pと点Rが初めて出会うのにかかった時 間は、点Qと点Rが初めて出会うのにかかった時間の２倍 でした。点Rの動く速さは点Pの動く速さの倍 です。   解説：P＋RとQ＋Rの出会うまでの道のりの比は3：2で、かかる時間の比は2：１なので、それぞ れの速さの比は3/2：2/1＝3：４となる。 Pの速さを�@、Qの速さを�Bとおくと、�@＋R＝３、�B＋R＝4  これより、�@＝0.5   0.5＋R＝３より、R＝2.5 P＝3−2.5＝0.5  よって、2.5÷0.5＝5倍 答え　 ５倍 [5]　Aは２桁の整数で,A×Aを15で割ると１余ります。このようなAは全部で個あります。 解説：A×Aは15で割ると1余るので、一の位は１か６。 書き上げてみると、 112,142,162,192,212,242,262,292,312,342,362,392 412,442,462,492,512,542,562,592,612,642,662,692 712,742,762,792,812,842,862,892,912,942,962,992 また、３で割っても５で割っても１余るので、この中で３の倍数の二乗になっているものは省く(赤 字)。 よって、36−12＝24個 答え 24個 [6] ２以上の整数Aに対して、Aの約数をすべてかけ合わせてできる数を[A]と書きます。 例えば、[6]＝1×2×3×６＝３６です。 B＝６のとき　  です。 また、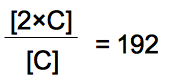 となる2以上の整数Cは　　　です。 解説：[2×6]/[6]＝ (1×2×3×4×６×12)/(1×2×3×4)＝48・・・�@ 　C＝2X×3Y、C=2X＋1×3Yの とき、約数の一覧表は次のようになる。 1 2 22 ・・ ２X 2X＋1 1 1 2 22 2X＋1 3 3×１ ３×２ ３×22 ・・ 3×２X 3×2X＋1 32 32×2X＋1 ・・ 3Y 3Y 3Y×2 3Y×22 ・・ 3Y×2X 3Y×2X＋1 ブルーの部分の積が、192＝26×3 であるので(それ以外は分母分子で共通のなので約分されて消える)、 X＝１のとき、22×(3×22)×(32×22) のように192にはなれない。 X=2のとき、23×(3×23)=192  となり、このときY＝1である。 すなわち、C=22×31=12 である。・・・�A 答え 　　�@48　　�A１２  [7] Xは３桁の整数で、どの２つの位の数も異なります。Xを７倍すると４桁の整数ABCDを作ることができ、 A>B、B>C、C>D、D>0 となりました。 このとき、Xはです。 解説：　PQR×７＝ABCDより、R=1のとき、条件を満たすABCが決まらない。 R＝２のときも同様。 R＝3のとき、PQ3×7＝ABCDより、P＝9とすると、9Q3×7より、 Q＝0となり、903×７＝6321 で条件に合う。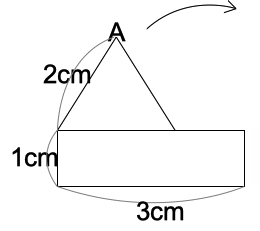 答え　903   [8] 縦の長さが1cm、横の長さが3cmの長方形と、１辺の長さが2cmの正三角形が、図のように置かれています。 正三角形が長方形の周に沿って、すべることなく図の矢印の向きに回転し、はじめて元の三角形の位置 に戻るまで移動します。このとき頂点Aが動いてできる線の長さはcmです。ただし、 円周率は22/7とし、１辺が2cmの正三角形の面積は7/3㎠とします。 また、頂点Aは元の位置に戻るとは限りません。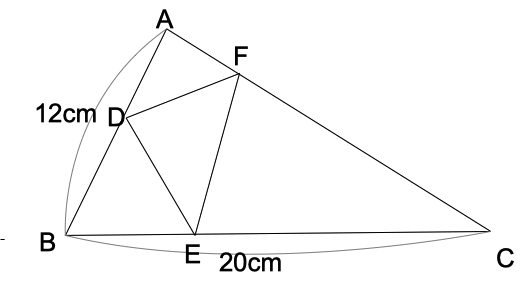 解説：4π×1/3＋２π×1/4＋4π×1/3＋7/2π×1/4＋4π×7/12＝(11 /8＋40/8)π＝561/28cm 答え　 561/28 [9]　下の図で、三角形ABCの面積は80㎠、三角形ADFの面積は10㎠、三角形CFEの面積 は35㎠、FCの長さはAFの長さの３倍です。BFとDEの交わる点をGとするとき、GFの長さは BGの長さの倍です。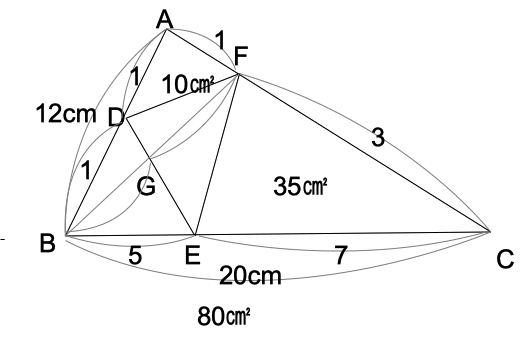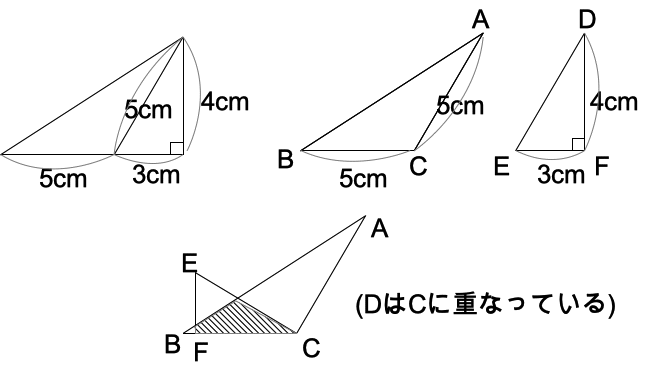 解説： 面積比公式より、35/80＝3/4×□より、  □＝7/12 また　10/80＝1/4×□より、  □＝1/2 よって、△BDE＝80×1/2×5/12＝50/3㎠ すなわち、△DEF＝80−(10＋35＋50/3)＝55/3㎠ よって、BG：GF＝50/3：55/3＝10：11 答え　 11/10倍 [10]　直角三角形を図のように三角形ABCと三角形DEFに切り分けます。これら２つの三角形 を図のように重ねたとき、斜線部分の面積は、㎠です。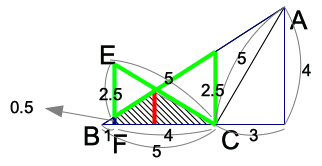 解説： 上図のように、4cm×1/8＝0.5cm、4cm×5/8＝2.5cm よって、 緑のちょうちょ相似の相似比が、(3−0.5)：2.5＝1：1であることがわかる。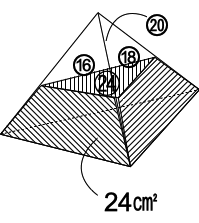 赤い線の長さは、(0.5＋2.5)÷2＝1.5cmなので、 5cm×1.5cm÷2−1cm×0.5cm÷2＝3.5㎠ 答え　 3.5㎠ [11]　下の図のように、三角すいの形をした 容器があり、４つの面の面積は、16㎠、18㎠、20㎠、24㎠です。 この容器にはいくらかの水が入っています。この容器を４つの面のいずれかが水平な地面につくように 置きます。容器の内側の面のうち水にぬれる部分の面積が最も大きくなるように置いたとき、水にぬれ る部分の面積は60㎠になります。水にぬれる部分の面積が最も小さくなるように置いたとき、水にぬ れる部分の面積は㎠になります。 解説：(1) 最大のとき下図のようになり、水にぬれている側面積は、60−24＝36㎠となる。�O＋�Q＋�S＝が水にぬれていない 側面積であり、(16＋18＋20)㎠−36㎠＝18㎠＝となり、�@＝1/3 ㎠ (2)最小のとき下図のようになり、すきま部分は(1)のときと合同になるので、�Q＋�S＋㉔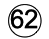＝＝1/3㎠ ×62＝62/3㎠である。よって、(16＋18＋20＋24)−62/3＝172/3㎠となる。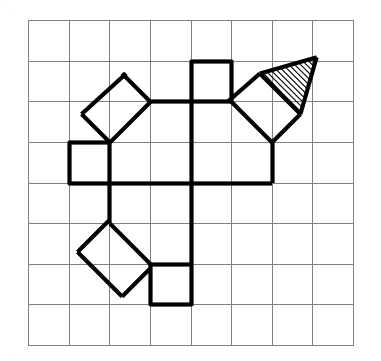 [12]　ある立体の展開図を、幅が3cmの方眼紙に書くと、下の図の太線のようになりました。斜 線をつけた三角形は正三角形です。また、正方形でない四角形の面はすべて長方形です。この立体の体 積はです。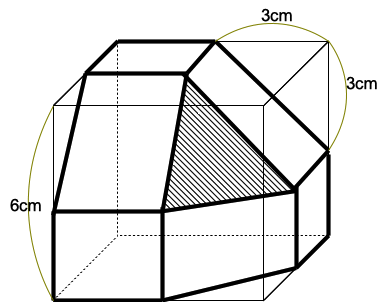 解説： 五角柱＋三角柱＋四角柱＋三角すいの順に、 (6×6−3×3÷2 )×3＋3×3÷2×3＋(3×6−3×3÷2)×3＋3×3÷2×3×1/3＝153 ㎤ 答 え153 ㎤