[中学受験算数ー穴あき立方体の切断]
![]() 次の上図のように、立方体を各辺の中点を通っ
て切断した切断面の面積と、下図のように同じ立方体を3方向に反対側まで穴をあけた立体を同じように切断したときの切断面の面積との比を答えなさい。
次の上図のように、立方体を各辺の中点を通っ
て切断した切断面の面積と、下図のように同じ立方体を3方向に反対側まで穴をあけた立体を同じように切断したときの切断面の面積との比を答えなさい。
(能開公開テスト)
![]() 解説
解説
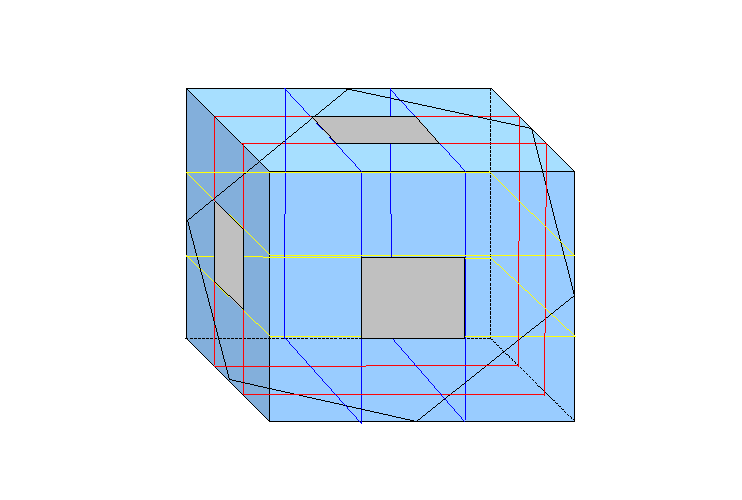
横方向の2つの赤い面と切断面との交線が赤い太線、たて方向の2つの青い面と切断面との交線が青い太線、水平方向の2つの黄色の面と切断面との交線が黄色 い太線でそれぞれ表されます。これらの太線を使って、穴の切断面はまず赤2本と黄色2本と青2本で囲まれた中心部の正六角形があり、赤2本と青2本で囲ま れたひし形、赤2本と黄色2本で囲まれたひし形、黄色2本と青2本で囲まれたひし形を重ね合わせた形になります。なぜなら”穴”はそれぞれ2つの赤い面、 青い面、黄色い面で囲まれた部分だからです。上図のように黒い太線で囲まれた部分は全部で6カ所あるので(もとの切断面正六角形)、合同な正三角形の個数 を数えると穴の部分は2カ所、それ以外は7カ所あるので、求める比は9:7です。
答え 9:7
考察
切断面は何個の小さな立方体を切るかという問題でも使う方法ですね。例えば赤い面と切断面の六角形の辺との交点は4点ありますが同じ平面上にある2点は結 ぶという考え方で慎重に結んでいくと赤い太線が書けます。他の太線も同様です。