図のような板ゴムをクリップではさんだものを用意する。
ゴム、クリップの重さは考えない。
ゴムについても、ばねのようにかかる力と伸びが比例するものとし、どの方向に引っ張っても伸び方に違い はなく、引っ張っても厚さは変化しないものとする。厚さが一様な一辺12cmの正方形のゴムシートAが あり、これに100gのおもりをつるすと1.2cm伸びた。
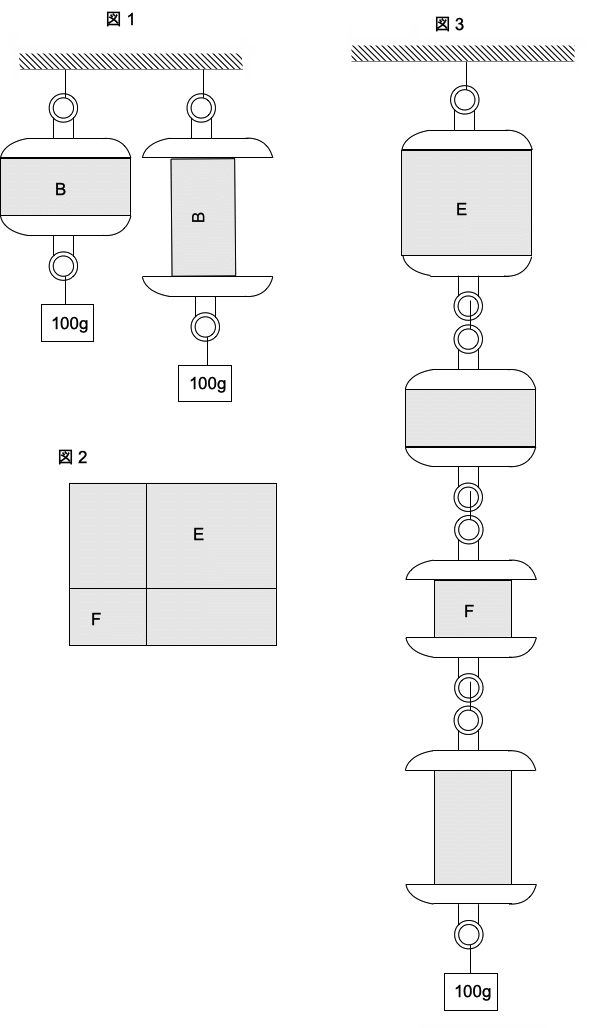
Aを2枚の長方形Bに二等分し、図1のようにそれぞれ100gのおもりをつるすと、伸びはそれぞれ 0.6cm、2.4cmになった。これは、Bを直列または並列につなぐともとのAになることから考えら れる。
図2のように、Aを4枚に切り分け(E,Fは正方形で、Eの方が大きい)、向きを変えずにたてにつな ぎ、図3のように100gのおもりをつるすと全体で6.4cm伸びました。Eの一辺は何cmですか。
「図 1のようにそれぞれ100gのおもりをつるすと、伸びはそれぞれ 0.6cm、2.4cmになった。」とあるので、伸びはたての長さに比例 し、横の長さに反比例している。
EとFは正方形なので、伸びは1.2cm×1÷1=1.2cmと なり、残り2枚の長方形の伸びは、6.4cmー 1.2cm×2=4cmである。
残りのたて長の長方形のたてをPcm横をQcmとすると、 1.2cm×P÷Qだけ伸びて、横長の長方形では、 1.2cm×Q÷Pだけ伸びる。
すなわち、1.2cm×P÷Q+1.2cm×Q÷P=4cm となる。
P÷Q=□とすると、 1.2×(□+1/□)=4
これより、□+1/□=10/3
□=3となる。
たて+横=12cm で、た て÷横=3すなわち、たて=横 ×3だから、横×3+横=横 ×4=12cmが成り立つ。
よって横=3cm、た て=3cm×3=9cm