搶戝帥妛墍拞妛俀侽侾係擭丂嶼悢4斣
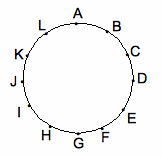
丒丂嵟弶丄揰P偼揰A偵偁傝丄捈慄ℓ偼捈慄BH偲堦抳偟偰偄傞丅
丒丂愒偺僗僀僢僠傪墴偡偲丄捈慄ℓ傪懳徧偺幉偲偟偰丄揰P偼懳墳偡傞揰偵摦偔丅
丒丂惵偺僗僀僢僠傪墴偡偲丄捈慄ℓ偑揰O傪拞怱偵帪寁夞傝偵30亱夞揮偟偨屻丄捈慄ℓ傪懳徧偺幉偲偟偰丄揰P偼懳墳偡傞揰偵摦偔丅
偨偲偊偽丄愒惵惵偲僗僀僢僠傪墴偡偲丄揰P偼A仺C仺C仺E偲摦偒傑偡丅偙偺偲偒丄師偺栤偄偵摎偊側偝偄丅
(1) 2夞僗僀僢僠傪墴偟偨屻丄揰P偼偳偺揰偵偁傝傑偡偐丅偁傝偊傞偡傋偰偺揰傪摎偊側偝偄丅
(2)丂徣棯
(3)丂13夞僗僀僢僠傪墴偟偨屻丄揰P偑揰E偵偁傞傛偆側僗僀僢僠偺墴偟曽偼慡晹偱壗捠傝偁傝傑偡偐丅
(1)丂愒傪R丄惵傪B偲昞偡偲丄RR仺A丄RB仺C丄BR仺A丄BB仺C偲偄偆寢壥偵側傞丅
摎偊丂A偲C
(3)丂(1)
傛傝丄2夞僗僀僢僠傪墴偡偲RR傑
偨偼BR偺偲偒丄傕偲偺揰偵傕偳傝丄RB傑偨偼BB偺偲偒丄2傔傕傝恑傓偙偲偑傢偐傞丅偙傟傪侾憖嶌偲偡傞偲
摓拝揰E偐傜媡栠偟偱峫偊偰丄12夞亐2夞亖俇憖嶌慜偵偝偐偺傏傞偲丄揰P偺偄傞応強偼丄E,G,I,K,A,C偺偳傟偐偵側傞丅偙
偺偆 偪嵟弶偺侾夞僗僀僢僠傪墴偟偰揰P偑摓払偱偒傞偺偼丄C偐E偟偐側偄丅偙傟偱応崌暘偗偟偰丄
(鶣)丂1夞栚
偱C偵摓払偟偨偲偒丒丒丒偁偲俇憖 嶌偱俀傔傕傝恑傔偽傛偄偺偱丄2傔傕傝恑傓偙偲傪仜丄傕偲偺揰偵傕偳傞偙偲傪亊偱昞偡偲
仜亊亊亊亊亊偺傛偆偵側傝丄仜偺埵抲偱俇捠傝丄仜偑
RB傑偨偼BB偺俀捠傝偁傝丄亊偑RR傑偨偼BR偺俀捠傝偁傞偺偱丄6亊(2亊2亊2亊2亊2亊2)亖384捠傝偲側傞丅
(鶤)丂1夞栚偱E偵摓払偟偨偲偒丒丒丒偁偲俇憖嶌偱12傔傕傝丄傑偨偼侽傔傕傝恑傔偽傛偄偺偱丄仜仜仜仜仜仜傗丄亊亊亊亊亊亊偺傛
偆偵 側傝丄偦傟偧傟丄2亊2亊2亊2亊2亊2亖64捠傝偱偁傞丅傛偭偰丄64亄64亖128捠傝偲側傞丅
埲忋偐傜丄
384亄128亖512捠傝偲側傞丅丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摎偊丂512捠傝