塗り分けの問題　　　　　　　　　　　　　プロ家庭教師のページへ

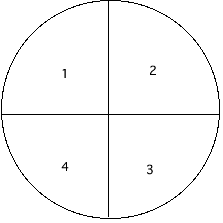
4色以内でぬり分けます。何通りのぬり分け方がありますか。ただし、 回転はしないものとしま す。

　誤答例 (さて、どこが違うか考えてみましょう！)

いわゆるダメダメ解法でやってみます。
１の部分は何色でもよいので、４通り。２の部分は１で使った色はダメなので、それ以外の３色が使えて３通り、３の部分は２で使っ た色 はダメなので、それ以外の３色が使えて３通り、４の部分は３と１以外の２色がつかえるので２通り。
よって、４×３×３×２＝７２通り

理由はこのページの最下部にあります。

解説
　単純に積の公式ではできません。同じ色をぬる部分で場 合わけをします。

1,3同色のとき　　4×3×2＝24通り

2.4同色のとき　　24通り

1,3と2,4にそれぞれ同色をぬるとき　　4×3＝12通り

すべて異なる色をぬるとき　　　　4×3×2×1＝24通り　

よって、24×3＋12＝84通り　　　　　　84通り

考察

同色をぬるときは、同色をぬる場所 で場合分けをするのが定石です。

　 誤答例の疑問点の回答

この問題の図では、ぬり分け問題なのにぬり分けしないでよい部分があ ります。
それは１と３、２と４の部分です。解説にもあるように１と３を違う色でぬり分ける場合と、同じ色を使いぬり分けない場合は明らか に異なります。
ダメダメ解法が使えるのは、となりあう部分はすべてぬり分ける必要がある場 合だけです。
たとえば次のような場合です。

この場合は、４×３×２×２＝48通り　となります。