均質で一様な重さ240g、長さ50cmの棒PQを図のように壁にもたれかかるように床に置きました。
棒PQのQから10cmのところに600gのおもりをつるしました。
おもりをPの方に動かしていったところ、棒がすべりだし、棒がななめにつり合わなくなるのは、おもりがPから何cmより近いところに きた ときですか。
ただし、棒と床の摩擦力が、床が棒を支える力の半分より大きくなることはありません。

下線部より、「棒と床との摩擦力=床が棒を支える力×0.5」のとき限界で棒はすべりだす。
Pが壁に接する所を支点として、モーメントのつりあいの式をつくる。
上下方向の力のつりあいから、床が棒を支える力は、240g+600g=840g である。
図のように、かかる力と支点までの距離は力と垂直な方向の距離をか ける ことでモーメントを求めることができる。
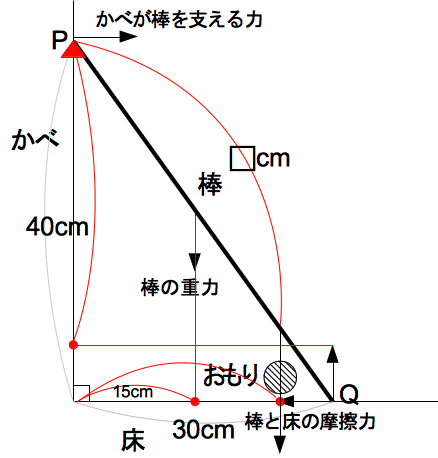
840g× 30cm=棒と床の摩擦力× 40cm+240g× 15cm+600g×□cm×3/5 → 3:4:5の辺の比を使う
ここで、棒と床の摩擦力=840g÷2となるときすべりだすので、上にあてはめて計算すると、25200= (840÷2)×40+3600+360×□ となる。
□=40/3cm
答え 40/3cm