中学受験、既約 分数の和      

中 学受験プロ家庭教師のペー ジへ

応用公式19

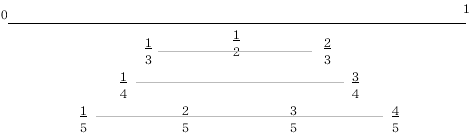
このように、既約分数は左右対称にあらわれます。こ のことから、既約分数の和は外側から内側に向って対称に足して行きます(ガウス公式)。

例えば、上図で、1/5＋2 /5＋3/5＋4/5＝(1/5 ＋4/5)×4÷2＝2　となります。

(問い)

1から300までの整数のうち で、2でも3でも5でも割り切 れない整数の個数とその和を求めなさい。

　　　　(奈良学園改)

解答

aが2でも3でも5でも割り切れない整数であるということは、a を分子、2,3,5の最小公倍 数30を分母とする分数が、既約分数(それ以上約分できない分数)であるということになります。

0と1の間にある既約分数は、

1／30、7／30、11／30、13／30、17／30、 19／30、23／30、 29／30

の8個で、同様に1と2の間にある既約分数も8個です。したがっ て、0と10のあいだにある既 約分数は8個×10＝80個あります。よって、1から300までの整数のうちで2でも3でも5でも割り切れない整数の個数は 80個です。

ところで、0と10のあいだにある既約分数のうちで、最小の既約 分数は1/30で、最大の既約 分数は299/30です。したがって、ガウス公式により、その総和は

(1/30＋299/30)×80÷2＝10×80÷2＝400 となります。ところで、求めた いのは分子の和だから、400×30＝12000

(問い)

同じように考えて、1から840までの整数のうち、2でも3でも 7でも割り切れない整数の個数 と、その和を求めなさい。

解答

12×20＝240個　　20×120×42＝100800

算数定理公式集へ