格子 点

応用公式18

次の図で、A地点からB地点まで行く最短の方法は

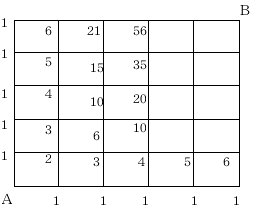
のように、1つ前の地点(すぐ左とすぐ下)の場合の数の和を、そこの地点に順に書いていけばよい。

(問い)

上図を完成して、A地点からB地点まで行く最短の方法が何通りあるか求めよ。

解答解説へ

---

解答 　

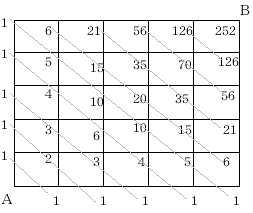
252通りです。斜めの 線の数字をたどっていくと、対称性に気付くと思います。これをパ スカルの三角形といいます。

　

考察

　他の考え方をしてみると、AからBまで到達するには、横に5区間、たてに5区間進めばよいこ とになります。例えば、横、横、横、たて、たて、たて、たて、 横、横、たて　といった感じです。

つまり、10区画から5区画を横として選べば、たては自動的 に決定します。つまり、10個から5個を選ぶ組み合わせで、10×9×8×7×6÷(5×4×3×2×1)＝252通り　となります。

問題にもどる

もどる