中学受験、円と 正方形　　　　　　　　　　　　　

中 学受験プロ家庭教師のペー ジへ

基本公式11

正方形の面積は、直角三角形4つ分の面積として求められるので、

ア×ア＝半径×半径÷２×４＝半径×半径×２　よって、半径×半径＝ア×ア÷２

このとき、円の面積＝円周率×ア×ア÷２

　

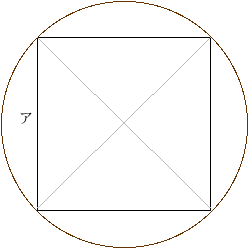
(問い)　上図で、正方形の一 辺ア＝４cmのとき、その4つ の頂点を通る円の面積を求めなさい。

解答 　

3.14×4×4÷２＝25.12㎠

(問い)　次の図で、小さい円の円周は、大きい円の中心を通って います。大きい円の面積が 314平方センチのとき、小さい円の面積は何平方センチですか。ただし、図の中の四角形は正方形です。 (関西学院)

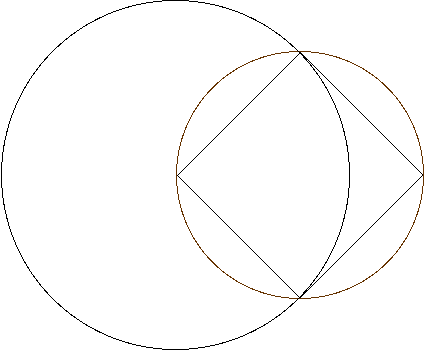
解答

小さい円の面積は　円周率×半径×半径÷2＝314÷２＝157 ㎠

算数定理公式集へ