中学受験、体積 比　　　　　　　　　　　　　　　　

中 学受験プロ家庭教師のペー ジへ

応用公式5

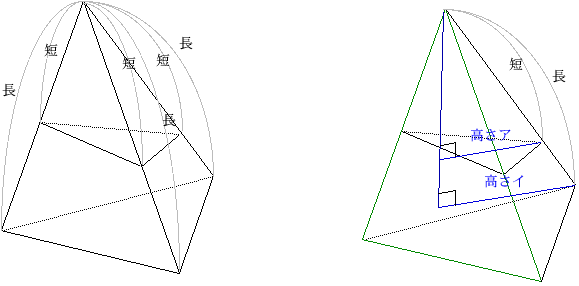
前ページの三角形の面積比の公 式を、三角すいに拡張したのが 次の公式です。

小三角すいの体積：大三角すい の体積＝(短×短×短)：(長 ×長×長)

なぜでしょうか。右図のように みどりの三角形を底面と考え、 頂点から図のように底面に垂直に青い補助線をひきます。すると、高さアが小三角すいの高さに、高さイが大三角すいの高さにな ります。このとき、ピラミッド の相似より高さア：高さイ＝短：長　となり、みどりの底面の面積比の短×短：長×長に、この高さの比の短×長をかけると上記の公式になります。

(問い)下の図の立体は正四角すいといい、底面が正方形で、 OA,OB,OC,ODの長さはす べて等しい。また、E,FはそれぞれOB,ODを３：１の比に、GはOCを３：２の比に分けている。このとき、EGFAを通 る平面により分けられた正四角 すいの２つの部分のうちOを含む部分の体積と正四角すいの体積の比をもとめよ。　(灘中学　改)

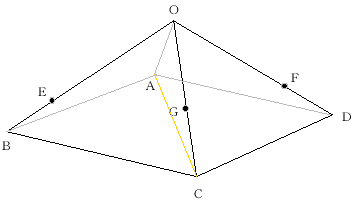
解答 　三角すいOABCと三角すいOACDに分けて考える。

OE×OG×OA：OB×OC×OA＝3×3×1：4×5×1＝9：20 　　　　(9＋9)： (20＋20)＝9：20

考察　　A点はOAを1：0に分けると考えると、この公式が使え ます。

四角すいや円柱では、高さの平均を求めて、底面積にかけると体積 が求まります。

算数定理公式集へ