円すい台　　　　　　　　　　中 学受験プロ家庭教師のペー ジへ

応用公式1

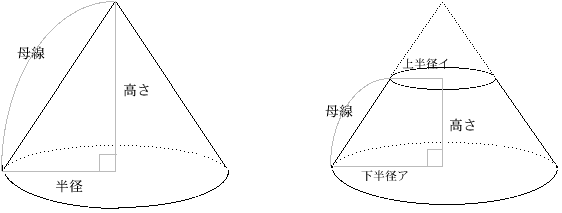
円すいの体積＝底面積×高 さ÷３　　　円すい台の体積＝円周 率×(ア×ア＋ア×イ＋イ×イ)×高さ÷3

側面積＝母線×半径×円周率　 　　　　　　　　　　側面積＝ 母線×(ア＋イ)×円周率

特に、円すい台の側面積は、覚えておくと便利です。

(問い)　

上図の円すい台で、半径アが6cm,半径イが3cm、母線が 5cm、高さが4cmのとき、この 円すい台の体積と表面積をもとめなさい。ただし、円周率は3とします。

解答　
３×(６×６＋６×３＋３×３)×4÷３＝252㎠

　　　側面積と底 面積の和をもとめると

　　　５×(６＋ ３)×3＋６×６×３＋３×３×３＝270㎠

考察

この表面積の公式は、展開図を使わないでもとめられるところがい いですね。展開図でもとめると きは、

円周部分×半径÷２の公式を使います。それも忘れたときは中心角をもとめることになります。

(問い)

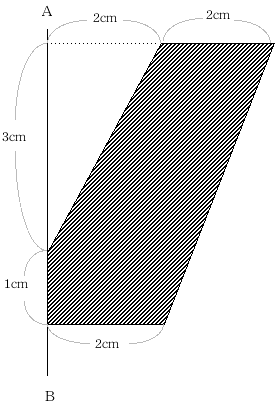
次の図の斜線を引いた図形を直線ABを軸として1回転してできる 立体の体積を求めなさい。ただ し、円周率は3.14として、小数第２位まで求めなさい。　 (ラ・サール)

解答

斜線部と左右対称の図形を作って１回転する とこのような立体ができます。

円すい台から空洞の円すいの体積を引けばよいから、

3.14×(4×4＋4×2＋2×2)×(3＋1)÷3ー 2×2×3.14×3÷3＝104.67 ㎤

もどる