中学受験、 自転公転          プロ家庭教師のページへ
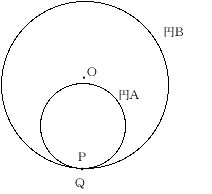
　小円Aが大円Bの内側を回転します点PはAの円周上に点QはBの円周上にあり、円A、円Bの 円周の長さ は、それぞれ56cm、96cmです。また、点Oは円Bの中心です。

(1)　点Pが、点Qと重なる点から出発してから、ふたたび点Pが点 Qと重なるまでに、円Aは、何 回転しますか。また、このとき、出発後円Aは点Qを何回通りますか。

(2)　点Pが出発後100回目に円Bの円周と重なる時、角POQの 小さい方の大きさは何度です か。

解 説

(1)　思ったほど回転数が少ないことが分かりますか。１回転も していません。

　　小円 が大円のまわりを一周するのに、外回りでは1回転多くなり、内回りでは1回転少なくな る。
　　96÷56＝12/7回転　12/7ー1＝5/7回転・・・1周あたり　よって5回転となる。
　　また、7周するので、7ー1＝6回通る。　　　　　　　　　　答え　6回

(2)　円Aがその円周の100周分進むので、円Bのまわりを　 56×100÷96＝58周とあと 1/3周する。

　　半径OQ に対して半径OPは120°の角をつくる。　　　　　　　　　答え　120°

考察

　(1)では、円Aがその円周の 12/7周分を進んで円Bを1周 してきたことになる。このとき、円Aは地球の中心に対しては1回転少ない5/7回転したということ。コインを回転させれば分かる ように、内回りでは進行方 向と自転方向が逆になるので1回転分少なくなる。外回りでは、進行方向と自転方向が一致するので１回転分多くなる。一方(2)で は、円Bの中心Oに対する 回転の角度を聞いているので、”何周分”の考え方をしている。”何回転”は地球に対して、”何周分”は大円の中心に対して、とい うふうに、しっかり区別す ること。

算数定理公式集へ