中学受験、ダイヤグラムの対称 性      

　ある川のA地から12kmはなれた下流にB地があります。AB間を下図のよう に往復する船P,Qがあります。船の静水上の速さは同じです。出発して2時間35分後にBから7.2kmのところで2度目に すれちがいました。船の上る速 さと流れの速さをもとめなさい。

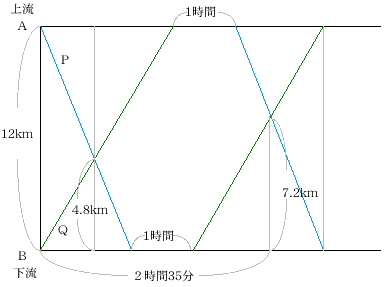
解説

　グラフをさかさまにしても、元に戻る。グラフの対称性から、1回め の出会いはB地から　 12ー 7.2＝4.8kmの地点となる。このことから、上り下りの速さの比は　２：３となる。またPは1時間35分の間に12km下り 7.2km上った。つまり 道のりの比は　5：3となる。以上を表にまとめると

	上り	下り
速さ	2	3
みちのり	3	5
時間	9	10

上の表で、みちのり÷速さ＝時間　より　３÷２＝3/2　　 ５÷３＝5/3　　3/2：5/3＝ 9：10　となる。

よって、7.2km上るのに　1°35′÷19×9＝3/4時間かか り　7.2÷3/4＝ 9.6km/時の速さとなる。

また、下りは　9.6×3/2＝14.4km/時の速さで、流れの速 さは　(14.4ー9.6)÷ ２＝2.4km/時

　　　　　　　　　　　　　　　　　　　　　　　　　　　答え 　上り9.6km/時　流れの 速さ2.4km/時

考察

　ダイヤグラムが威力を発揮する問題です。ま た、みちのりの比を速さの比で割って、時間の比を出すことが思い付きにくいかもし れませんが、表解をふだん使い慣れていれば簡単でしょう。

算数定理公式集へ