中学受験、仕切 り水入れ　 　　　　　プロ家庭教師のページへ

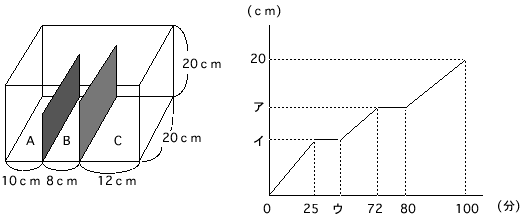
長方形の仕切り板PQで仕切られた直方体の形をした水そうがあり ます。AとCの部分にそれぞれ 一定の割合で同時に水を入れていきます。グラフはこのときの水を入れ始めてからの時間と、Aの部分の水面の高さの関係をあら わしたものです。
　(1)　図のア、イ、ウにあてはまる数を求めなさい。

　(2)　Cの部分には毎分何立方センチの割合で水を入れました か、

解説  

　AとBの部分の底面積の比より　25分×18/10＝45分　 　　　ウ＝45

仕切りの高さと、そこまで入れ るのにかかった時間は比例するので、

　　　　80：100＝ア：20　　　ア＝16ｃｍ
　　　　45：72＝イ：16　　　 イ＝10ｃｍ

100分で20ｃｍ入っているので、後はいもずる式にもとまる。 折れ線の最後から考えよう。

　また、AとCで12000立方センチ÷100分＝120立方セ ンチ/分　入り

　Aで2000立方センチ÷25分＝80立方センチ　入っている ので　　120−80＝40㎤//分　　　

40㎤/分

考察

折れ線の最後、結果どうなったかが重要です。水入れの問題では、 逆戻しで考えると答えに早くた どり着ける場合が多いです。45分から72分のグラフも、80分から100分のグラフも、そのまま伸ばせば0の点を通りま す。左側にあるしきりを取れば、 1つの直方体に水を入れるのと同じになるので、当然です。0の点を通るグラフは比例のグラフです。そこに気が付けば、仕切り水入れの問題では、横軸の時間の数 値と、たて軸の深さの数値で比例式をつくると瞬 時に解決です。